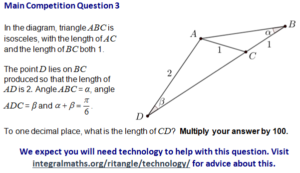
A RITANGLE problem
When RITANGLE advises you to use technology to answer a question, you know it’s going to get messy.
So, with some trepidation, here goes:
(As usual, everything below the line may contain spoilers.)
It’s easy enough to do this in Geogebra - but somehow a little bit unsatisfactory to move the points around until they work. It is possible to do analytically - but only if you can solve quartics!
I can’t solve quartics. However, Wolfram|Alpha can - and I think that’s an acceptable use of technology in this case.
Here’s how I solved it.
Using the sine rule on the big triangle BAD gives $\frac{\sin(\alpha)}{2}=\frac{\sin\br{\frac{5}{6}\pi}}{1 + CD}$, which leads to $\sin(\alpha)=\frac{1}{1+CD}$.
In triangle ACD, angle ACD is $2\alpha$, and angle ADC is $\piby 6 - \alpha$. Using sine rule on this gives $\frac{\sin(2\alpha)}{2} = \frac{\sin\br{\piby 6 - \alpha}}{1}$.
We can tidy this up: $\sin(\alpha)\cos(\alpha) = \frac{1}{2}\cos(\alpha) - \frac{\sqrt{3}}{2}\sin(\alpha)$.
However, we know what $\sin(\alpha)$ is, so we can throw it in. Doubling everything: $2\frac{\cos(\alpha)}{1+CD} = \cos(\alpha) - \frac{\sqrt{3}}{1+CD}$.
Rearranging to make $\cos(\alpha)$ the subject leaves us with: $\cos(\alpha)\br{1 - \frac{2}{1+CD}}= \frac{\sqrt{3}}{1+CD}$.
Multiply both sides by $(1+CD)$ to get $\cos(\alpha)= \frac{\sqrt{3}}{CD-1}$.
Now we’re getting somewhere! We have expressions in terms of $CD$ for $\cos(x)$ and $\sin(x)$, which means we can turn to the identity $\sin^2(x) + \cos^2(x)\equiv 1$.
This is going to be messy, but no matter: $\frac{1}{(1+CD)^2} + \frac{3}{(CD-1)^2}=1$
Multiplying up, and letting $x=CD$ (as we should have done earlier, but I can’t be bothered going back to change it now), we get $(x-1)^2 + 3(1+x)^2 = (1+x)^2(1-x)^2$.
That leads to $4x^2 + 4x + 4 = x^4 - 2x^2 + 1$, or $0=x^4 - 6x^2 - 4x - 3 = 0$.
According to the Wolf, this has real solutions around -2.19 (which makes no sense in this context) and 2.80, which is the answer we’re after.
And, for some reason, we have to multiply it by 100, to which I say “shan’t”.