Ask Uncle Colin: A Set Square Mark
Dear Uncle Colin
I just bought a new set square and noticed it had a couple of extra marks - one at seven degrees and one at 42 degrees. Have you any idea what those are for?
- Don’t Recognise Extra Information Engraved on Calculus Kit
Hi, DREIECK, and thank you for your message!
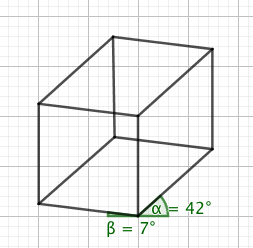
I didn’t know this, and had to look it up. It turns out, one convention for drawing things in three dimensions uses exactly these angles: lines going “across the way” are 7 degrees above the (negative) $x$-axis; lines going “back the way” are 42 degrees above the (positive) $x$-axis; and vertical lines go directly up. A cube might look like this:
Isn’t that pleasing?
But why those particular angles?
It’s not just for simplicity and aesthetics, although those are factors. I’m told they make it unlikely for lines to intersect at important points (although I don’t quite see how that’s more true for these angles than any other pair).
My favourite reason, though, is that it’s possible to find these angles quite simply using squared paper: because $\tan(7º) \approx \frac{1}{8}$, you can approximate the slope by moving eight squares to the left and one square up from your chosen point. Similarly, $\tan(42º)\approx \frac{9}{10}$, so moving ten squares across and nine squares up would get you an excellent approximation to the gradient you need.
Hope that helps!
- Uncle Colin