Dear Uncle Colin,

Sector ABC

I got stuck on this sector question, which asks for the radius of circle $P$, which touches sector $ABC$ as shown. I’m given that $ABC$ is a sector of a circle with centre $A$ with radius 12cm, and that angle $BAC$ is $\frac{\pi}{3}$. My answer was 3.8cm, but apparently it should be 4cm. - Someone Explain Circles To Otherwise Reasonable Student

Hi, SECTORS, and thanks for your message!

The answer is indeed 4cm, and here’s how you can work it out.

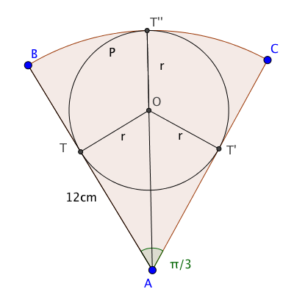
Solution

I started by drawing radii from the tangent points on AB and AC to the centre of the circle, and the line of symmetry of the sector. This gives us a radius to each tangency point - but it also gives us two right-angled triangles.

ATO is right-angled at T, and has an angle of $\frac{\pi}{6}$ at A, by symmetry. That means (because $\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}$), $OA=2OT=2r$.

Aha! That means line segment $AT”=3r=12$cm (because it’s a sector of a circle) and $r=4$cm as a result.

Hope that helps!

- Uncle Colin

* Updated 2017-06-28 to fix a typo. Thanks to @singinghedgehog for the correction.