Basic Maths Skills: The Falklands Islands, Percentages and Bounds
I have no particular view on the sovereignty of the Falkland Islands. Or rather, I get so muddled up between my distaste for colonialism and the right of self-determination that I don’t know what to think.
In any case, I was interested by the recent referendum results in which the results were reported as 99.8% of the turnout voting ‘yes’ and three people voting ‘no’, results that wouldn’t have looked out of place under Saddam Hussein. Not that I’m comparing the queen to Saddam Hussein. Really, that wouldn’t be at all nice ((I’ll leave determining who gets the worst of the comparison as an exercise for the interested reader)).
Instead, what with exams coming up, it got me wondering a couple of things. The obvious question is, what was the turnout? The second-most obvious question is, if the 99.8% is correct to 3 significant figures, what’s the highest and lowest the turnout could have been?
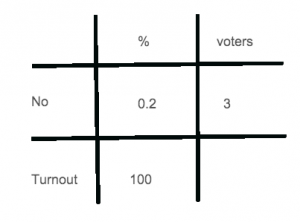
The original percentage question isn’t all that hard, although it needs a bit of thought: the three people represent 0.2% of the Falklands’ electorate ((at least, of those that bothered to vote)) - and a little work with the Table of Joy gives you:
The sum works out to be $100 \times 3 \div 0.2$; you can tidy that up by multiplying the top and bottom by 10 to give $1000 \times 3 \div 2$, which is $1,500$. Sounds about right for the population of some rocks in the South Atlantic.
Working out the upper and lower bounds isn’t too hard, either: what we can say about the percentage $p$ is that it’s between 99.75 (inclusive) and 99.85 (exclusive): $99.75 \le p\% \lt 99.85$. ((Don’t be tempted to put $99.84$. It could be higher than $99.84$. And $99.84\dot(9) = 99.85$, so don’t bother with that, either.))
That means the percentage $q$ of ‘no’ voters is between $0.25$ (inclusive) and $0.15$ (exclusive): $0.15 \lt q \le 0.25$.
We can do the same Table of Joy sum, simply changing the number after the $\div$:
The upper limit is $100 \times 3 \div 0.15 = 10,000 \times 3 \div 15 = 2,000$ (multiplying top and bottom by 100); the lower limit is $100 \times 3 \div 0.25 = 400 \times 3 = 1,200$ (multiplying top and bottom by 4).
That tells you, the turnout $t$ of the Falklands Island referendum was somewhere between 1,200 (inclusive) and 2,000 (exclusive), or - if you prefer it with symbols: $1,200 \le t \lt 2,000$.
Alternatively, I could have looked up the results in a newspaper: the turnout was 1,516.
* Edited 2014-09-06 to add a footnote and fix LaTeX.