$\cos(72º)$, revisited: a geometric method
Some months ago, I wrote about a method for finding $\cos(72º)$, or $\cos\br{\frac{2\pi}{5}}$ in proper units. Almost immediately, the good people of Twitter and Facebook - notably @ImMisterAl (Al) and @BuryMathsTutor (Mark)- suggested other ways of doing it.
Let’s start with Mark’s method, which he dissects in his book GCSE Maths Challenge ((I have not yet read the book, but think highly of Mark and trust that it’s a good one.)).
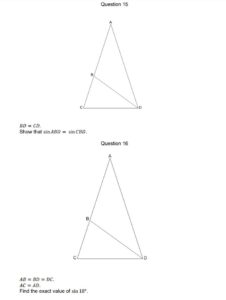
Looking at Q16 here, we have three isosceles triangles. ACD and DCB are similar (they’re both isosceles, and base angle C is the same in both). If we call angle CAD $\theta$, then ABD is $180º - 2\theta$, so CBD and DCB are both $2\theta$.
That means the three angles in ACD add up to $5\theta$, which must be 180º; $\theta$ is therefore 36º.
Suppose the length BD (and therefore CD and BA) is one unit, and the length BC is $x$. We can do some trigonometry!
Applying the cosine rule to the big triangle ACD, we have $\cos(72º)=\frac{1 + (1+x)^2 - (1+x)^2}{2(1+x)} = \frac{1}{2(1+x)}$.
Doing the same to the smaller triangle CBD, we have $\cos(72º)=\frac{1+x^2-1}{2x} = \frac{x}{2}$.
Let $\cos(72º)=C$ for the purposes of algebra, and we have $2C=x$ from the second equation. Substituting this into the first gives $C=\frac{1}{2+4C}$.
Rearrange this to give $4C^2 + 2C - 1 = 0$, and $C$ drops out of the quadratic formula as $C=\frac{-1 \pm \sqrt{5}}{2}$; we know $\cos(72º)>0$, so only the positive branch makes sense.
Therefore $\cos(72º) = \frac{\sqrt{5}-1}{2}$.
I like this method a lot - it drops out super-neatly. However, it feels a bit like the triangles have appeared by magic; it’s easy to prove it once you have the scaffolding in place, but I wouldn’t have come up with the scaffolding on my own.