The Maths Behind... Cakes
“Cooking,” said my friend Liz in a recent Facebook post, “is one of the activities where maths is most useful in my everyday life.” She added this picture:
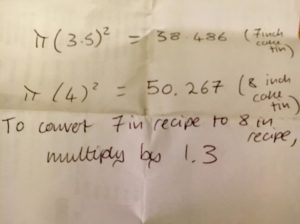
I’ve got several reasons for wanting to share this.
1. It’s pretty much a model answer
Imagine you’re in a GCSE exam, and the paper asks:
Liz has a recipe that calls for a cake tin with a 7-inch diameter, but only has an 8-inch diameter tin available. How should she adjust the recipe, assuming all cake tins are the same depth?
This is a perfectly plausible question, incidentally, although I’d be surprised to see inches feature.
Liz has worked out the area of the top of a 7-inch cake, the area of the top of an 8-inch cake, clearly stating the sums she’s done and what each means, and written down a succinct conclusion that answers the question.
There are a couple of things I’d have liked to see done differently - had this been an exam rather than a scrap of paper in the kitchen. I’m not going to mark Liz down for them, obviously.
Firstly, I’d have liked to see a more precise mention of what she was calculating (at least a mention of area); secondly, the 1.3 appears a bit miraculously, so explaining 50.267 ÷ 38.486 ~ 1.3 wouldn’t go amiss.
One last thing I liked: Liz used a reasonable degree of accuracy. The calculation gives 1.306 (of which more later), but 1.3 is a much more sensible thing to multiply by in the kitchen, especially using metric measures as any sensible person would.
2. She missed a trick
That sounds harsher than I mean it; Liz’s approach is exactly what I’d recommend to almost anyone who asked me for help to make that calculation.
However, it’s not how I’d do it. As a friend of Liz’s, Mark Ruddell, points out in the comments: all you need to know is that area is proportional to length squared. The clue is in the units: area is in metres squared (or, in this case, inches squared), so it makes sense that - say - tripling the diameter would increase the area ninefold.
In this case, Liz’s tin has $\frac{8}{7}$ the diameter of the recommended one, so its area is $\br{ \frac{8}{7}}^2 = \frac{64}{49}$ as large - which is a shade over 1.3.
(This idea, dimensional analysis is exceptionally important in applied maths. I’ve seen physicists figure out ballpark estimates by saying “energy is kilograms metres squared per second squared. Mass is this, length scales are this, time scales are this” then multiply and divide as appropriate.)
3. There’s a Ninja angle
Whoosh. The light barely catches a glimmer of the blade as The Mathematical Ninja wields the sword, almost faster than the eye can see.
“Slightly smaller slice for me, thanks.”
The blade whirrs again. “You know that $\frac{64}{49}=1.\dot{3}0612244896959183673469387755102040816326\dot{5}$, don’t you? We talked about it before.”
“I got as far as $1 \frac{15}{49}$.”
“That’s a fair start. I’d call it $1 \frac{30}{98}$.”
“Oh! And that starts with 1.30… and each next pair of digits is double the pair before?”
“Pretty much. The trick is to add one if your pair is over 50, and ignore any hundreds that show up - so 30 goes to 61, goes to 122 but we’ve already accounted for the 1 and ignore it.”
“I see. Is 1.3 acceptable?”
The Mathematical Ninja’s eyes narrow.
“Would the cake be any nicer if I’d multiplied by 1.30612244 whatever?”
The Mathematical Ninja tactfully changes the subject.
4. It’s super maths-positive
One of the things that brings me greatest pleasure is seeing someone say “LOOK WHAT I DID WITH MATHS!”
It’s made even better when someone doesn’t instinctively add “I’m not usually very good at maths”, but takes joy and pride in having figured something out.
Liz’s post made my day. Go Liz!