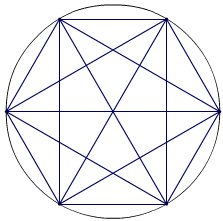
The Mystic Rose

[twit handle=’standupmaths’] pointed me at a puzzle by [twit handle=’sciencepunk’] at MathsJam: or at the Science Punk blog.

The question is: how many triangles are there in a ‘Mystic Rose’ shape like this one (right) - with six interconnected points.

I reckon there are 110.

I got this by splitting it up into different types of triangle, like this:

Triangle type

Number

Notes

One triangle

18

6 on the edge (isosceles), 12 at the corners (right-angled)

2T

18

12 x edge + corner (right-angled); 6 x double-corner (equilateral)

3T

12

Right-angled triangle along edge

4T

6

All the way along the edge (isosceles)

1 triangle, one quad

12

Right-angled triangle involving vertex and centre

3T 1Q

6

Equilateral triangle into middle

2T 2Q

6

Centre and two non-adjacent corners (isosceles)

2T 3Q

6

Isosceles triangle with two opposite corners

3T 3Q

12

Right-angled triangle with non-adj corners

5T 3Q

12

Right-angled triangle with three vertices

6T 6Q

2

“Star of David” equilateral triangles

Total:

110

I keep adding it up differently, but I’m pretty happy that it’s 110 now.

Note that all of the triangles involve at least one vertex. Apart from the “star of David” triangles in the middle, the isosceles/equilateral triangles come in groups of six and the right-angled (scalene) triangles come in groups of 12.