Why is the dot product the way it is?
(Thanks to Barney Maunder-Taylor for teasing me with this one.)
This question interests me for two reasons: Firstly, it’s a neat proof in its own right, and I’ll start by giving a little sketch of it. Secondly, though, even after Barney gave me the crux of the proof, it still took me an embarrassingly long time to figure it out. I’ll go on to explain where I got stuck and how I worked my way through it – which is probably more instructive than the proof itself.
The proof
In C4, it’s pretty much handed to you on a tablet of stone that
$\bb a \cdot \bb b = \left|\bb a\right|\left|\bb b \right|\cos (\theta)$
There is no need to question this miraculous bit of maths, as far as C4 is concerned; all you need to do is use it. But it’s nice to prove these things as an exercise; it makes the other proofs you might need to do easier if you practise ones you don’t need to do.
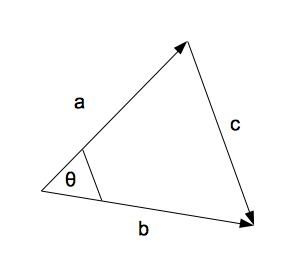
So, let’s start with a triangle. I’ve arbitrarily picked vectors $\bb a$ and $\bb b$, and joined them up with $\bb c$ on the far side.
If you remember your GCSE vector work, you’ll know that $\bb c = \bb b - \bb a$, because you can replicate $\bb c$ by going backwards along $\bb a$ and forwards along $\bb b$.
And what else do we know about triangles that has a cosine in it? That’s right, the clue’s in the name. And the cosine rule is in the formula book.
$a^2 = b^2 + c^2 - 2bc \cos (A)$
Although, of course, we’ve picked different letters for our sides and angles, and it applies to the lengths of the vectors rather than the vectors themselves. So, we can rewrite that as:
$\left|{\bb c}\right|^2 = \left|\bb {a}\right|^2 + \left|\bb b\right|^2 - 2\left|\bb a\right|\left|\bb b\right| \cos (\theta)$
We’re starting to get somewhere! We’ve got the $|\bb a||\bb b| \cos(\theta)$ we were after, which is good. Still a bit of spot the difference: we’ve got a $c^2$ knocking about that we don’t want, and we definitely don’t want a 2 in front of the $|\bb a||\bb b|$ bit. So let’s replace $|\bb c|$ with $|\bb b-\bb a|$ and see what happens.
$\left|{\bb b-\bb a}\right|^2 = \left|{\bb a}\right|^2 + \left|{\bb b}\right|^2 - 2\left|\bb a\right|\left|\bb b\right| \cos (\theta)$
By definition, $|\bb v|^2$ is just the squares of the components of $\bb v$ added together - so, for instance, $|\bb a|^2 = a_x^2 + a_y^2 + a_z^2$. Let’s expand all those squares out:
$(b_x - a_x)^2 + (b_y - a_y)^2 + (b_z - a_z)^2 = a^2_x + a^2_y + a^2_z + b^2_x + b^2_y + b^2_z - 2\left|\bb a\right|\left|\bb b\right|\cos(\theta)$
That’s a bit of a mess, but if we note that, for example, $(b_x - a_x)^2 = b_x^2 - 2a_x b_x + a_x^2$, all of those bracketed squares on the left and all of those squares on the right can be replaced with $-2a b$ on the right, with the appropriate subscripts:
$- 2a_x b_x - 2a_y b_y - 2a_z b_z = - 2\left|\bb a\right|\left|\bb b\right|\cos(\theta)$
Dividing it all by -2 gives exactly the dot product formula:
$a_x b_x + a_y b_y + a_z b_z = \left|\bb a\right|\left|\bb b\right|\cos(\theta)$
Draw a nice smug square at the end: you’re done! $\blacksquare$
My issue
My problem in this proof was that I’d forgotten my GCSE vectors stuff and didn’t spot straight away how to get rid of the c. (Barney had, generously, told me ‘it’s just the cosine rule!’ in a throwaway manner that was simultaneously impressive and irritating – a good trick to pull off for a maths tutor; he is an honorary ninja).
Like a thick detective, I took stock of what I knew:
- I need to get rid of that -2
- I need to come up with the dot product side of things from somewhere
- I’ve got a load of squares to get rid of
These things together pointed me at the answer. I know that $(x+y)^2 = x^2 + y^2 + 2xy$, which has the benefit of accounting for some squares AND possibly getting the dot product involved with a 2. My exact thought was ‘wouldn’t it be nice if I could make $c = b - a$ and then it’d all drop out perfectly.’ And after a moment’s thought, the ‘wouldn’t it be nice’ turned into ‘of course it is, you dolt’ and I got to put the slightly embarrassed square at the end of the proof myself.
* Edited 2018-05-31 for typesetting and readability.