A circle problem that succumbs to a circle theorem
A tweet from @GregSchwanbeck some time back asked:
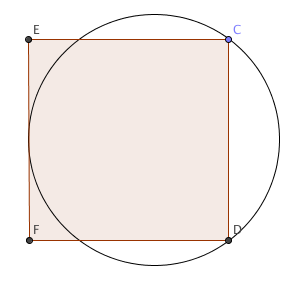
Does square or circle have greater perimeter? A surprisingly hard prob for HS: http://t.co/vwLIs26pcC #mathchat #math pic.twitter.com/Vpjop8yU7G
— Greg Schwanbeck (@GregSchwanbeck) March 16, 2015
The setup is: one side of a square is tangent to a circle, and two corners of the square lie on the same circle. Which is larger: the perimeter of the square or the circumference of the circle? (My labels are different to Greg’s. That’s his fault, obviously.)
The typical approach is to adopt some sort of algebraic approach, but I – having been trawling around for sneaky geometrical tricks to approximate $\pi$ – had a more elegant trick up my sleeve.
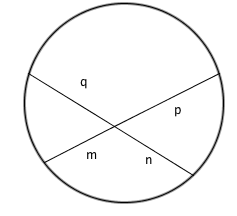
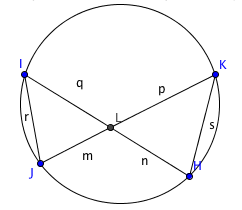
It involves a circle theorem that crops up in IGCSE but not at GCSE, relating to the lengths of the intersections of chords. If you have two intersecting chords of a circle (as pictured), the products of their parts are equal – that is to say, $mp = nq$ as drawn.
To prove this, note that triangle $LIJ$ is similar to $LKH$, by comparing angles, which means $\frac mn = \frac qp$, so $mp = nq$.
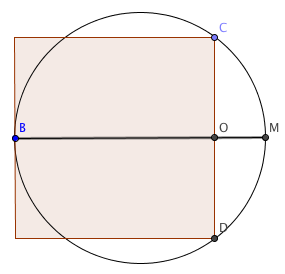
How does it help? Consider the diameter to the circle at the point where the square is tangent, $BM$ in the picture below. That’s a chord; so is $CD$, so $|CO| \times |OD| = |BO| \times |OM|$. If we assume for the sake of simplicity that the square has a side length of 8, then $|CO| = |OD| = 4$, while $|BO| = 8$. Using the theorem, $|OM| = \frac{8}{4} = 2$, so the diameter of the circle is 10 and the radius is 5.
The circumference of the circle is then $10π \approx 31.4$, while the perimeter of the square is 32 – so the square’s perimeter is larger.
That puzzle wasn’t enough for @tombutton, though: he asked:
Sphere goes through 4 vertices of a cube and midpoint of the opposite face. Which has greater surface area? pic.twitter.com/fUnSWgTfgu
— Tom Button (@tombutton) March 17, 2015
Happily, this falls to the same analysis, although it’s a bit harder to see (things in 3d usually are). The tangent point and two incident points that don’t share an edge (i.e., they’re diagonally opposite on one face) are on a circle which shares its centre with the sphere (and hence, its diameter is the sphere’s diameter). Again, if the side length is 8, the diagonal of the face is $8\sqrt 2$, so the product of the half-chords is $4\sqrt 2 \times 4 \sqrt 2 = 32$; the diameter splits up as 8 (from one face of the cube to the other) and 4 (using the theorem).
In this case, the radius of the sphere is 6, so the surface area is $4\pi r^2 = 108\pi$; the surface area of the cube is $6 \times 8^2 = 384$.
Which is greater? The ratio is $144\pi : 384$, which have a common factor of 48, making it the same as $3\pi : 8$. Since $3\pi > 8$, the sphere has the larger surface area.