Dear Uncle Colin,

I have an inequality that involves two pairs of modulus signs, and I can’t make head nor tail of it.

It’s ||3−x|−2x|≤9.

Please help!

-- Absolutely Bewildered, Driven Absolutely Barmy

Well, ABDAB, I’d normally recommend sketching something like this, but it’s not immediately clear where to start. It can be done, though.

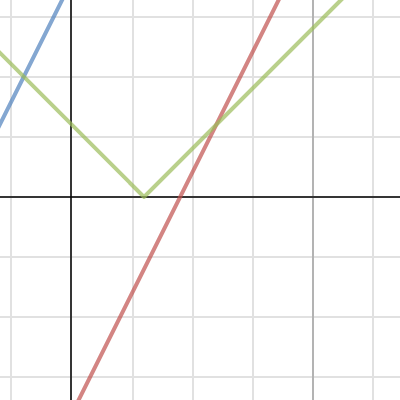
Taking the outermost modulus signs out, we can rewrite the inequality as −9≤|3−x|−2x≤9, or better yet, 2x−9≤|3−x|≤2x+9. All of those things are easy to draw:

We’re looking for where the green line lies between the other two; the first step towards that is to find out where the lines cross.

Where does |3−x|=2x−9? Well, if x<3, it’s 3−x=2x−9, giving 3x=12, or x=4 – but unfortunately, that doesn’t satisfy the restriction. If x>3, it’s x−3=2x−9, giving x=6, which does work.

How about where |3−x|=2x+9? Similarly, if x<3, it’s 3−x=2x+9, or 3x=−6 and x=−2. For x>3, x−3=2x+9, which gives the spurious answer of x=−12.

So, we have our two crossing points, at x=−2 and x=6, and know that our set of values lies between them (inclusively), giving us −2≤x≤6.

If we had any doubt about how the inequalities went, we could test a point in each region – showing that when x<−2, the inequality is false, it’s true in the range we just found, and it’s false when x>6.

Hope that helps!

-- Uncle Colin

* Missing inequality sign inserted 2016-02-10. Thanks to @realityminus3 for spotting it!