Ask Uncle Colin: Solving Trigonometric Equations
Dear Uncle Colin,
I’m trying to solve $2\cos(3x) = -\sqrt{2}$, for $0 \leq x \lt 2\pi$, but the answers I find are outside the specified interval, and obviously I miss the ones that are in the interval. How would you tackle this?
- Like A Puzzle, Like A Cosine Equation
Hi, LAPLACE, and thanks for your message!
Quite a lot of Ask Uncle Colin posts have a sense of “There’s More Than One Way To Do It”. This one is not one of those: I am here to lay down The One True Way, the way that finally made it work for me, and the one I use with any student who doesn’t have their own reliable way.
Step 1: Make the trig function equal to a number
In some cases, this involves factorising, but here it doesn’t: we just need to say $\cos(3x) = -\frac{\sqrt{2}}{2}$.
Step 2: Adjust your interval if necessary
The cosine argument here is $3x$, but the interval is given for $x$. In this case, we’re simply going to multiply everything by 3 to say $0 \leq 3x \lt 6\pi$ (that is, we’ll need three complete periods of the cosine graph.) I would also let $\theta = 3x$ to save on a bit of confusion.
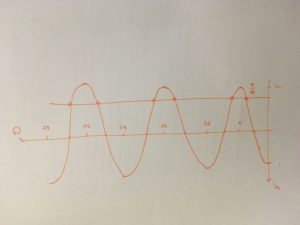
Step 3: Sketch the graph
Here, you’re sketching the graph of $y = \cos(\theta)$, with $0 \leq \theta \lt 6\pi$.
Your sketch doesn’t need to be perfect, it just needs to wibble up and down in roughly the right places - as long as it shows the turning points and crossing points clearly enough for you to see the symmetries, it’s a good enough sketch.
A quick aside on how I sketch this graph
-
Draw $x$- and $y$-axes, labelling the $x$-axis every $\pi$. (For cosine, these will be the turning points; for a sine graph, they would be the crossing points).
-
Mark on those turning points and the crossing points midway between them.
-
Join up the dots with a nice smooth curve.
-
Hastily label the axes before @realityminus3 notices.
You can also draw on the value you’re looking for: $y = -\frac{\sqrt{2}}{2}$, and mark where it crosses the curve.
Step 4: Use your brain or (if you must) your calculator to find a value
$\arccos\br{ - \frac{\sqrt{2}}{2}} = \frac{3}{4}\pi$, which (in this case) corresponds to the leftmost crossing.
Step 5: Use the symmetries of the graph to find the other values.
The first value is $\piby 4$ below $\pi$, and the next must be $\piby 4$ above it, which gives $\frac{5}{4}\pi$.
The graph repeats every $2\pi$, so the remaining solutions for $\theta$ are $\frac{11}{4}\pi$, $\frac{13}{4}\pi$, $\frac{19}{4}\pi$ and $\frac{21}{4}\pi$.
Step 6: Move the solutions back into the original domain.
We made $\theta$ up - it’s equal to $3x$. So we have $3x = $ (all of those multiples of $\pi$.)
To find $x$, we just need to divide them all by 3, which gives us $x = \frac{3}{12}\pi$, $\frac{5}{12}\pi$, $\frac{11}{12}\pi$, $\frac{13}{12}\pi$, $\frac{19}{12}\pi$ and $\frac{21}{12}\pi$. (The first and last of those can be simplified to $\piby 4$ and $\frac{7}{4}\pi$, respectively.)
All six solutions are back in the interval we wanted.
(After doing enough of these, you can start to generate and remember shortcuts. In my experience, having a reliable method you trust and understand beats any number of badly-memorised rules.)
Hope that helps!
- Uncle Colin