If you’ve read this blog for a while, you’ll know I’m a fan of @cshearer41’s puzzles (her book, Geometry Puzzles in Felt Tip, is available wherever etc). At a recent MathsJam, one jumped out of Chalkdust at us:

Four Hexagons by Catriona Shearer

(Image from Issue 10 of Chalkdust, a magazine for the mathematically curious.)

It’s a Catriona Shearer classic: there just doesn’t look like there’s enough information to solve it.

Spoiler: there is. And I’m going to spoiler it some more below the line.

Step 0: what do we know?

First things first: let’s write down the information we have.

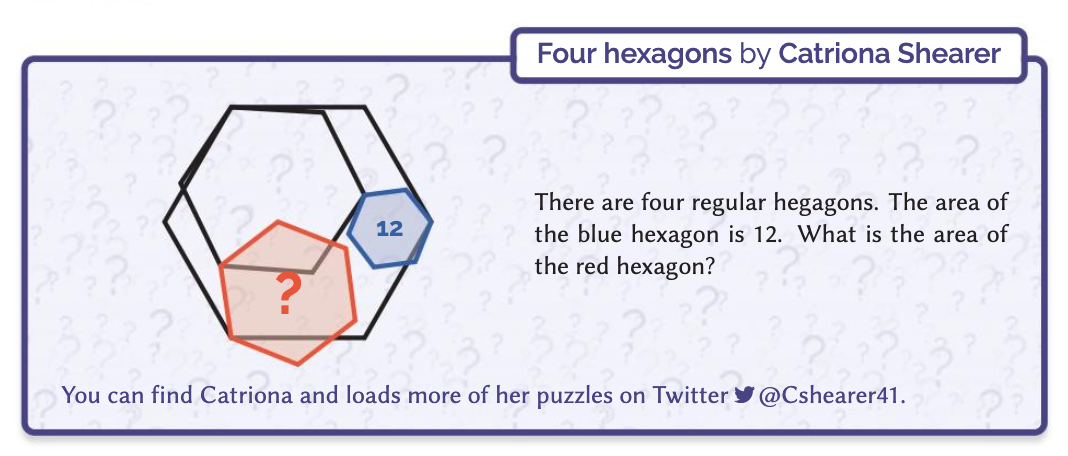
  • There’s a Small regular hexagon with area 12 units.
  • One of its vertices, A, is shared with a Huge Hexagon.
  • Another vertex, C (two edges away) is shared with a Big Hexagon.
  • Big Hexagon shares a vertex D, two edges away from C, with the Huge Hexagon.
  • Big Hexagon shares another vertex E (two away from C but the other way) with a Medium Hexagon.
  • The vertex F on Medium Hexagon adjacent to E is shared with Huge Hexagon, two edges away from A.

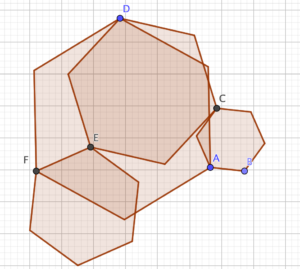
I don’t know that that helps immediately. Maybe a picture will?

Four Hexagons (ii)

Step 1: assume there’s an answer.

It’s a Catriona Shearer puzzle. There’s bound to be a simple answer.

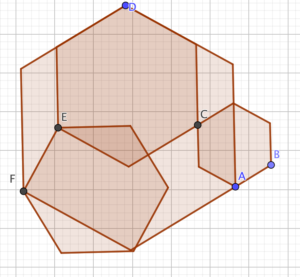
In particular, the hexagons are arranged haphazardly - where they are isn’t important. We can move them around, so long as we keep them all regular.

In particular, I can make it sorta-symmetrical by making two of the Big Hexagon’s edges partially coincide with the Huge hexagon.

Four Hexagons (iii)

Now it becomes clear: DEC is an equilateral triangle, and DFA is an equilateral triangle, so EF = AC.

AC, being a short diagonal of a hexagon, is 3 times as long as its edge - so the edges of Medium Hexagon are 3 times as long as those of Small Hexagon; its area is three times as big, so the area of the Medium hexagon is 36 units.

So that’s the answer… in the symmetric case. And presumably every case, but it feels a bit dissatisfying to leave it there, doesn’t it?

Step 2: generalise

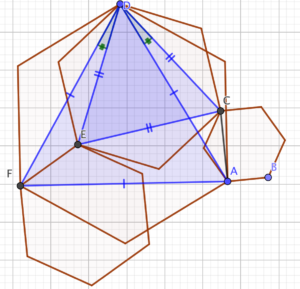
The triangle insight feels important, so let’s dim down the hexagons and put some triangles in their place.

Four Hexagons (iv)

With a bit of thought, we can find some congruent triangles! Angles FDE and ADC are equal, as are sides FD and DA; DE and DC are also equal to each other, so triangle FED is congruent to ACD - and AC = FE, which is what we wanted!

Like so many of Catriona’s puzzles, I enjoyed that one twice: first in finding an answer, and then in showing that it was the answer.

Did you tackle it any differently? I’d love to hear.

* Many thanks to @cshearer41 and @chalkdustmag for use of the puzzle.