A challenge question
A challenge question:
The curve with equation $y=e^{kx}$ is tangent to the curve with equation $y=x^2$. Find $k$.
Curves tangent to other curves? Well, why not! Tangent just means ‘touching’ – so as long as there’s a point common to both curves where the gradients are the same, we’re good.
So, we need to solve $e^{kx} = x^2$, and – for the gradients:,$ke^{kx} = 2x$.
Those look tricky. However, you can solve them by substituting the first into the second:
$k \left(x^2\right) = 2x$, so $k = \frac{2}{x}$. ((As @realityminus3 has pointed out, I’ve lost a ‘solution’ of $x=0$ – although it turns out to be extraneous, I should have accounted for it.))
Substituting that into the first equation gives $e^{2} = x^2$, so $x = \pm e$.
Lastly, put this back into the $k$ equation to get $k = \pm \frac{2}{e}$.
Click on the picture to play with it: 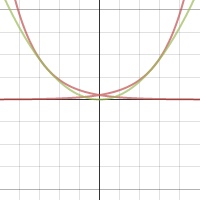
Edited 2015-06-18 to correct an oversight.