A Triangle In A Square
In a currently-recent (but by the time you read this, long in the past) Chalkdust ((It’s a magazine for the mathematically curious)), @cshearer42 gave a puzzle that caught my eye.
One of the things I love about Catriona’s puzzles is that you usually get two-for-the-price-of-one: there’s “getting the right answer”, which is not usually hard, and there’s “getting the answer elegantly”, which is rewarding.
Below the line are spoilers.
The right answer
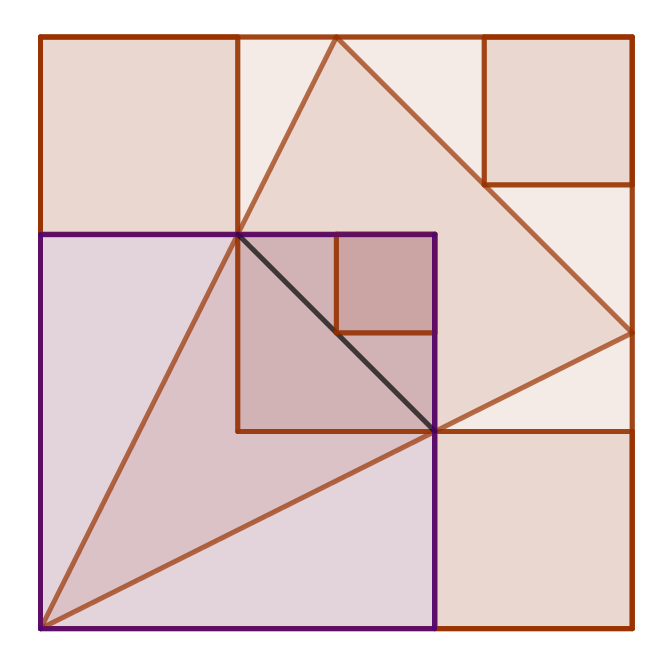
Tackling it tired, I took a bit of a sledgehammer to it: the line resting on the top-left of the lower-right 16-square has a gradient of $\frac{1}{2}$, so it cuts the outer square midway up the right edge.
Similarly ((ha!)), the other line from the bottom-left corner has a gradient of two and cuts the upper edge at its midpoint.
A symmetry argument means the target square’s lower edge is then three-quarters of the way up the main square; the big square’s edge length is 12, so the target square has side length of 3 and area 9.
Ugh.
The right answer
The insightful way - or rather, an insightful way, is to think about the purple square pictured. The oblique line I’ve drawn splits the middle square in half, so the square in the upper quarter has area 4.
BUT, that diagonal is parallel to the top-right side of the big isosceles triangle in the big square - which makes it similar to the triangle in the purple square. Since the purple square has sides two-thirds the length of the big square, the target square has sides three-halves as big as the upper-quarter square from the last paragraph - so the area is 9!
Did you find another nice method? I’d love to hear about it.