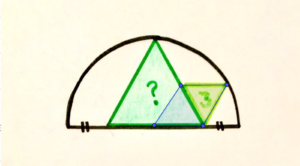
A triangle puzzle
Like everyone else on Twitter, I’m a sucker for a nice-looking question, and @cshearer41 is a reliable source of such things.
I particularly liked this one:
There are two equilateral triangles inside this semicircle. What’s the area of the larger one? pic.twitter.com/Nvy01z2j5f
— Catriona Shearer (@Cshearer41) November 7, 2018
Straight in with the instinct
“OBVIOUSLY 12.” It jumped out at me that the side of the larger triangle was double the smaller one. It’s a portion of a star-of-David.
But why is it? That turned out to cause me more problems than I expected – and in a @DavidKButlerUoA-inspired “show what you tried”, I’ll talk you through the methods I considered.
Is it really double?
The more I looked at it, the more doubtful I became. I drew a radius to the rightmost point of the smaller triangle. “Look, it’s a perpendicular bisector, so half the side of the large triangle is the same as the side of the small one!”
Who says it’s a perpendicular bisector? (It is, but I haven’t proved it).
Yuk
The best proof I could come up for it is this: reflect the triangles across the diameter, then the green angle at the centre is double the green angle on the circumference (which we know to be $\piby6$). We’d need to confirm that the lines involved are in fact straight (they are). The radius to the right-hand vertex of the small triangle is therefore at right angles to its leftmost side (yadda yadda isosceles yadda yadda bisector).
A sneaky rhombus
Something that eventually popped out at me was this blue shape here. The bottom-right corner has an angle of $\frac{2}{3}\pi$, and the top-right one of $\frac{1}{3}\pi$. The top and bottom sides are therefore parallel, making the shape a parallelogram.
Therefore, the top and bottom sides are the same length as each other; the left and right sides are the same length as each other, and we’re looking at a rhombus. In particular, the bottom-left half of the rhombus is congruent to the small equilateral triangle, and has a side length of half the big triangle.
So, the big triangle is the same size as four little ones.
I can’t help but feel I’m missing a trick here (I reject Pythagoras as overly ugly). Do you have a straightforward argument for why the side length has to be half?
* Edited 2019-05-13 to put in a missing image.