An alternative proof of the sin⁡(2x) identity

Uncle Colin recently explained how he would prove the identity $\sin (2x)\equiv 2\sin (x)\cos (x)$. Naturally, that isn’t the only proof.

@traumath pointed me at an especially elegant one involving the unit circle. Suppose we have an isosceles triangle set up like this:

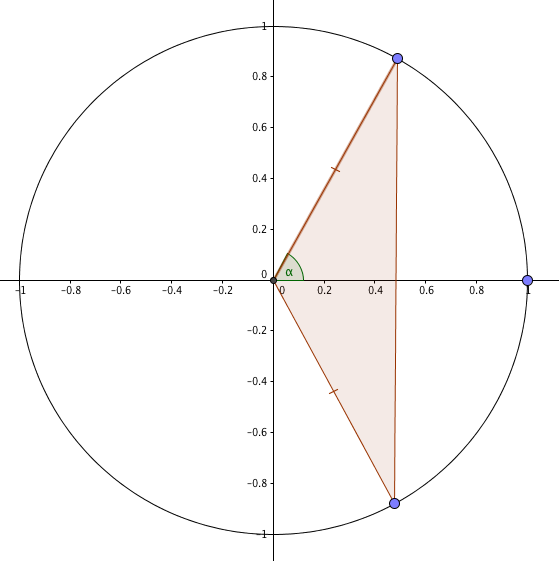The vertical ‘base’ of the triangle is $2\sin (\alpha )$ units; the perpendicular ‘height’ is $\cos (\alpha )$, both easily established from right-angle trigonometry or (you know) the definitions of sine (roughly speaking, how far up the angle takes you on the unit circle) and cosine (how far across). Its area is $\sin (\alpha )\cos (\alpha )$.

Now suppose we rotate the triangle by an angle of $\alpha$ around the origin like so:

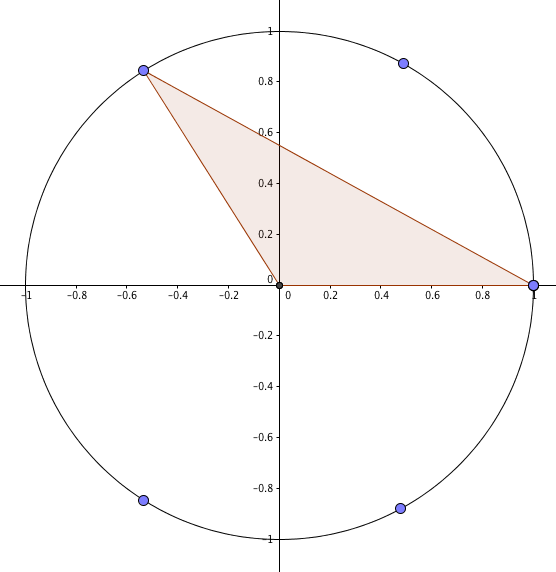
The horizontal base of this triangle is one unit, and the perpendicular height is $\sin (2\alpha )$, making the area of the triangle $\frac{1}{2}\sin (2\alpha )$.

We’ve only rotated it, so its area hasn’t changed – which means $\sin (\alpha )\cos (\alpha )\equiv \frac{1}{2}\sin (2\alpha )$. Double everything and boom! There’s your identity.

* Edited 2016-08-25 to link to the previous post.