Another of Alison's Ace Puzzles, Revisited
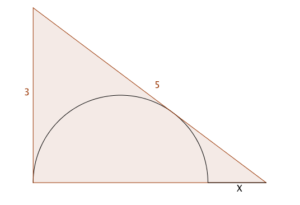
This is a guest post from @ImMisterAl, who prefers to remain anonymous in real life. It refers to the problem in this post: a semi-circle is inscribed in a 3-4-5 triangle as shown; find $X$.
As with any mathematical problem, my first thought was to sort out exactly what I know or can easily find, and what I want to know.
I know:
- we have a right angled triangle with all the side lengths given, and I could use trigonometry to find the angles if I wanted to
- we have a (semi)circle, so I could possibly use circle theorems for something
I want:
- the length $x$, which is the base of the triangle minus the diameter of the circle
Hmm. So, if I find the radius of the circle I can easily double that to get the diameter, from which I can find $x$. But how to get to that radius?
Since I know that I can find any angle in the triangle, that’s what I’ll focus on. Let’s call the top vertex of the triangle point $B$ and the vertex at the right angle point $D$. Let the centre of the circle be $C$ and the point of tangency be $T$.
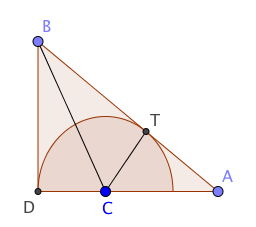
Drawing the line $BC$ forms two triangles, $BCD$ and $BTC$ which look as though they might be congruent. Are they congruent? Yes they are, since both these triangles are right-angled, and the Equal Tangents theorem tells us that $BD = BT$, and also $CD$ must equal $CT$ since they’re both just radii of the circle. That means the angle $CBD$ is half of angle $ABD$. That’s got to be useful, right?
(Confession time: At this point I reached for my calculator – yes, I know, and I’m sorry ((I want your maths badge on my desk by 9am tomorrow - Ed.)) – and I got it to tell me angle $ABD$, which I divided by 2 to give angle $CBD$. I then considered the triangle $BCD$ and used the trigonometry buttons on my calculator again to tell me the radius of the circle. But when I saw how simple the final answer was, I realised there must be a neater way.)
Let’s call the angle $CBD$ $\theta$, which would make angle $ABD$ equal to $2\theta$. Triangle $CBD$ then tells us that $\tan(\theta)=\frac{r}{3}$ and from triangle $ABD$ we get $\tan(2\theta)=\frac{4}{3}$. Ah, but I know an identity that links those two things. Exciting stuff! Let’s piece it all together. Here’s the identity:
$\tan(2\theta) = \frac{2\tan(\theta)}{1-\tan^2(\theta)}$
Substituting what we have into that gives us the equation:
$\frac{4}{3} = \frac{ 2 \left(\frac{r}{3}\right)}{1-\left(\frac{r}{3}\right)^2}$
This rearranges into the quadratic equation:
$2r^2 + 9r - 18 = 0$,
which has solutions $r=-6$ and $r=\frac{3}{2}$, and since the radius can’t be negative, $\frac{3}{2}$ must be our answer. From here it’s a simple step to show that $x$ equals 1.
Of course, I kicked myself when I later saw that using similar triangles gave a far more elegant solution, but I was pleased to use the double angle identity for $\tan$ in an actual problem. It’s always the identity that tends to get overlooked in my opinion.