Ask Uncle Colin: A Pair Of Toy Trucks
Dear Uncle Colin,
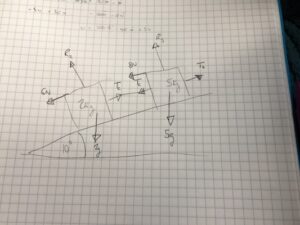
I have an exam question I don’t understand! There’s a toy truck of mass 5kg attached (by a rod) to another truck of mass 2kg on a slope at 10 degrees to the horizontal. The resistances to motion are 8N and 6N, respectively, and the whole thing is pulled up the slope by a string. The question says to show that the rod is always in tension so long as the trucks move up the slope. What’s your approach?
Toys Easily Negotiate Slope In Our Nursery
Hi, TENSION, and thanks for your message!
The first thing I would do is draw a picture. It would probably be a messy picture, like this one.
Pictures!
Since the trucks are moving up the plane, the resistance forces act down it. There’s an equal-and-opposite force in the coupling which I’ve drawn as a tension, but could be a thrust (if so, $T_c$ will wind up negative, and that’s perfectly ok in a rod. In a string, it would be a problem).
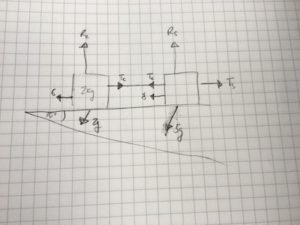
I like to think of a grid with this kind of question, with lines parallel and perpendicular to the surface. In fact, by turning the page, I can draw it like this:
The two weights are the only ones off of the grid - and I only really care about the ‘horizontal’ components of those (that is, parallel to the plane). Those are $2g \sin(10º)$ and $5g \sin(10º)$, respectively.
Equations of motion!
Then I can write down equations of motion for the parts of the system, and the system as a whole:
- Upper truck: $T_s - T_c - 8 - 5g\sin(10º) = 5a$
- Lower truck: $T_c - 6 - 2g\sin(10º) = 2a$
- System: $T_s - 14 - 7g \sin(10º) = 7a$
The acceleration could be in either direction, but as long as the velocity is upwards, these equations hold true.
Calculation
Starting with the system as a whole, $a = \frac{T_s}{7} - 2 - g\sin(10º)$.
Substituting this into the lower truck equation gives: $T_c - 6 - 2g\sin(10º) = 2\left( \frac{T_s}{7} - 2 - g\sin(10º)\right)$, or $T_c = \frac{2}{7} T_s + 2$
Since $T_s \ge 0$ (it’s a tension in a string), $T_c \ge 2$ and is in tension as long as the motion is uphill.
Hope that helps!
- Uncle Colin