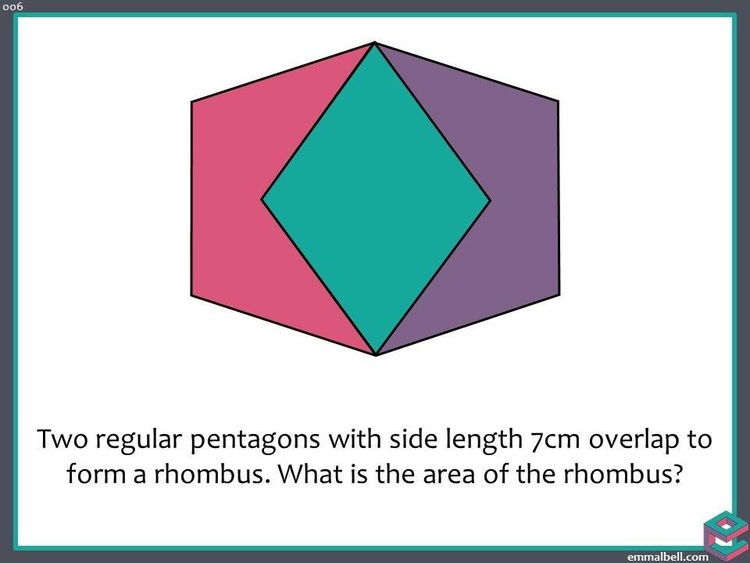
Ask Uncle Colin: A pentagonal rhombus
Dear Uncle Colin,
I’ve carelessly interlocked a couple of regular pentagons together like this and need to find the area of the overlap because of reasons. For still other reasons, I don’t want to use trigonometry. How do I negotiate my way through this minefield?
Trigonometry’s Always Overrated
Hi, TAO, thanks for your question! I’m sure you have perfectly good reasons to avoid saying “It’s clearly $49 \sin\left( \frac 35 \pi \right)$” but you’re right – we can do better!
There’s a $\phi$ knocking around here somewhere
One angle of attack is to notice that the longer diagonal of the rhombus is $7\phi$, where $\phi = \frac{1 + \sqrt{5}}{2}$ is the Golden Ratio. This took me an embarrassing amount of time to prove, but it comes out quite neatly.
In the image below, triangle ION is isosceles, which means NO is 7.
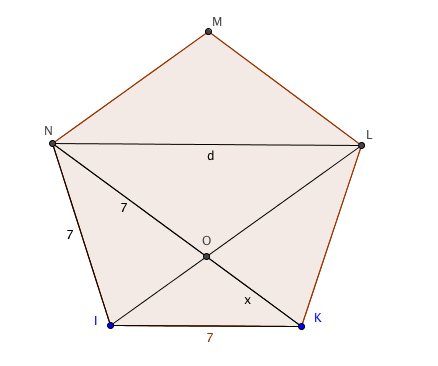
Call OK $x$; then by similar triangles, $\frac{x}{7} = \frac{7}{d}$, while $d = 7 + x$.
Eliminating $x$ gives $d-7 = \frac{49}{d}$, or $d^2 - 7d - 49 = 0$.
This has two solutions, $d = \frac 72 \left(1 \pm \sqrt{5}\right)$.
Only the positive one makes sense, which is $d = 7\phi$.
Now for the rhombus
The rhombus is made of two triangles, each of which has side lengths 7, 7 and $7\phi$. This calls for Hero\[n\]’s formula!
The semiperimeter is $7 + \frac{7}{2}\phi$ ((I wish the puzzle had had a nicer number than 7!)). I’m going to take a factor of $\frac{7}{2}$ out and make it $S = \frac{7}{2}\left(2 + \phi\right)$. That makes the square of the area $S(S-a)(S-b)(S-c) = \left(\frac{7}{2}\right)^4 \left(2 + \phi \right) \left(2 - \phi \right) \phi^2 $.
Let’s sort that $\phi$ out : $\left(2 + \phi \right) \left(2 - \phi \right) \phi^2 = \left( \frac{5 + \sqrt{5}}{2} \right) \left( \frac{3 - \sqrt{5}}{2}\right) \left( \frac{1 + \sqrt{5} }{2} \right)^2$. Oo, looky, another factor to come out ($\frac{1}{16}$), making the bit at the beginning $\left(\frac{7}{4}\right)^4$.
That leaves us (ignoring the constant for now) with $ \left( 5 + \sqrt{5} \right) \left( {3 - \sqrt{5}} \right) \left( {1 + \sqrt{5} } \right)^2$, which expands to $\left(10 - 2\sqrt{5}\right)\left(6 + 2\sqrt{5}\right) = 40 + 8 \sqrt{5}$.
So, where were we? $A^2 = \left(\frac{7}{4}\right)^4 \left( 40 + 8 \sqrt{5} \right) = \frac{2401}{32} \left(5 + \sqrt{5}\right)$, so $A = \frac{49}{4} \sqrt{\frac{5 + \sqrt{5}}{2}}$.
That’s the area of the triangle, so the area of the rhombus is $A = \frac{49}{2} \sqrt{\frac{5 + \sqrt{5}}{2}}$.
What’s that, Ninja-chops?
The square root of 5 is about 2.236, so we’re looking at the square root of 3.618 in that last factor. 3.618 is pretty much the square of 1.9 (which is 5% less than 2); multiplied by $\frac{49}{2}$ (which is 2% less than 25), we get about 7% less than 50, which is 46.5. (The correct answer is 46.6. Not too shabby.)
\– Uncle Colin
\* Thanks to Emma Bell for setting the problem. \* Edited 2016-02-03 to put in missing images. Thanks also to @dragon\_dodo for pointing out the omission.