Dear Uncle Colin,

I’m stuck on a trigonometry question: find $\cos\br{\frac{1}{2}\arcsin\br{\frac{15}{17}}}$.

Any bright ideas?

- Any Rules Calculating Some Inverse Notation?

Hi, ARCSIN, and thanks for your message!

That’s a nasty one!

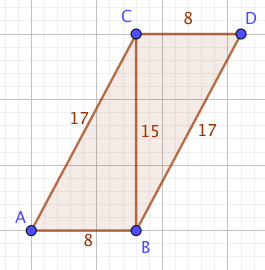
Let’s start by thinking of a triangle with an angle of $\arcsin\br{\frac{15}{17}}$ - the opposite side is 15 units, the hypotenuse 17 and the adjacent side (according to Pythagoras), 8 units.

How do we split that angle in half? There are ways of doing it with sums, but I’m in a triangles sort of mood today. We’re going to turn our triangle into a rhombus.

That's not a rhombus!

If you turn a copy of your triangle upside-down and put the length-15 sides next to each other, you get a… parallelogram, which isn’t quite what we need. The slanted sides are 17 units long, but the horizontal ones are only 8.

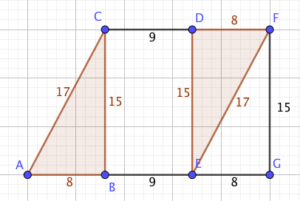
We can fix that by sliding the upside-down triangle along nine units so that the bottom edge becomes 17 units long as well.

The line AF bisects the angle CAB, which is exactly what we need: triangle AGF is right-angled at G, so its legs have length 15 and 25, and a hypotenuse of $5\sqrt{34}$.

That's a rhombus!

Therefore, the the cosine we want is $\frac{25}{5\sqrt{34}} = \frac{5}{\sqrt{34}}$.

More generally

Given any trigonometric ratio for an angle $\theta$ (assuming it’s in the first quadrant), you can easily determine $\tan(\theta)$ by considering a triangle with the relevant side lengths and applying Pythagoras. Suppose $\tan(\theta)=\frac{a}{b}$ and the hypotenuse is $c$.

To find $\tan\br{\frac{\theta}{2}}$, you need to move the rotated triangle across by $c-b$ to make a rhombus, putting the far corner of the rhombus $b+c$ across, and still $a$ up.

That means $\tan\br{\frac{\theta}{2}} = \frac{a}{b+c}$, or $\frac{a}{b+\sqrt{a^2+b^2}}$.

Alternatively, if $\tan(\theta)=t$, $\tan\br{\frac{\theta}{2}}= \frac{t}{1+\sqrt{1+t^2}}$.

Hope that helps!

- Uncle Colin