An awkward inequality
Solve $\sqrt{|x|-3} > x-4$
Difficult, as the man said. Difficult, difficult, lemon difficult.
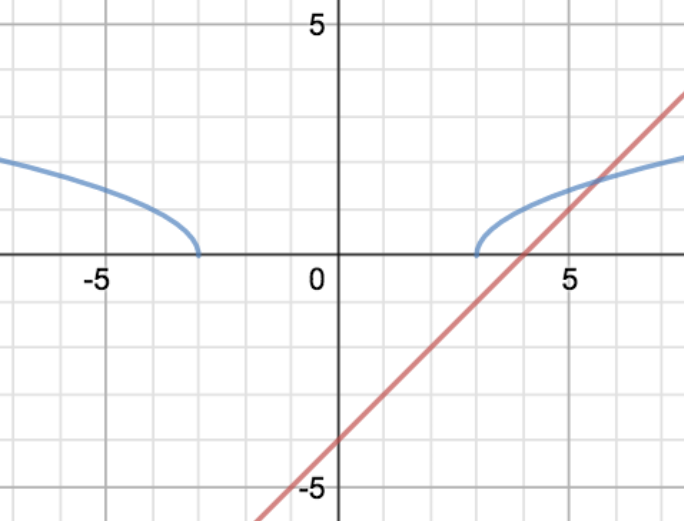
It’s not that it’s tricky to solve it - it’s just… fiddly. Let’s start by drawing the graphs. The right-hand side is easy enough: it’s a straight line with gradient 1, through the point $(0,-4)$. The left-hand side is trickier, and let’s go through it in detail, using the graph-sketching rules: DATAS.
D is for domain: where is this blighter defined? The square root only works if the argument is at least 0, so $x$ has to be either at least $3$ or at most $-3$ - so the function is defined everywhere except for $-3 < x < 3$.
A is for axes: where does it meet them? Obviously, it doesn’t meet the $y$-axis, because it’s not defined for $x=0$, but it meets the $x$-axis at $x= -3$ and $x=3$.
T is for turning points: luckily, it doesn’t have any.
A is for asymptotes, and it doesn’t have any of those, either.
S is for shape: the square root graph normally goes up and to the right, getting gradually shallower. The right-hand branch does that; in the second quadrant ($x \le -3$), it does the mirror-image, going up and to the left.
Right, good. Now, where is the curve above the line? Obviously, everywhere in the left-hand branch is good, so the equation holds for all $x \le -3$. On the right, the curve starts above the line (when $x=3$, the curve has $y=0$ and the line has $y=-1$), but eventually the line and the curve cross. Where? Well, we need to solve for that. $x$ is positive, so we can ignore the modulus signs and solve:
$\sqrt{x-3} = x-4$
Square both sides: $x-3 = x^2 - 8x + 16$, or $0 = x^2 - 9x + 19$
That doesn’t factorise, so let’s use the formula:
$x = \frac{9 \pm \sqrt{81 - 76}}{2}$ $= \frac{9\pm \sqrt{5}}{2} $ $\simeq \left\{ 5.168, 3.382\right\}$
Two answers? That doesn’t fit with the graph. One of them doesn’t make sense, though: when $x=3.382$, the line is below the $x$-axis, so that’s not a valid solution to our original question.
So, the line and the curve cross at $x = \frac{9+\sqrt{5}}{2}$. What does that mean for our inequality?
It means that - on the right hand branch - the inequality holds for $3 \le x < \frac{9+\sqrt{5}}{2}$, as well as $x \le -3$ on the left-hand branch.
Lemon difficult
That’s a really nasty modulus inequality question, which - had we not drawn the graph and thought about which answers made sense, we’d have been in all kinds of trouble. Notice also that, even though the original inequality was strict (<), the final inequalities are partly inclusive ($\le$), because of the nature of the square root function.