Cav, Catriona and some hexagons
It’s always fun to tackle a puzzle from one of Cav’s posts - in this case, a Catriona Shearer puzzle; it looks like my solutions are completely unrelated to his, although in reality I tend to sneak the odd peek and take some inspiration ((I crib from his answers, is what I’m saying. It’s ok. It’s research.))
I also liked that Cav shared many of his failed attempts. I’m not going to do that, but I’m certainly going to acknowledge that getting this right and getting it neat took several hours.
In any case, here is the puzzle in question:
Have a go yourself before you read on - below the line are spoilers.
A diagram
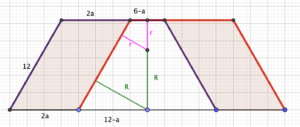
Here’s an after-the-fact, accurately constructed diagram of the top half, which needs a little bit of explanation:
I’ve only taken the top half because of symmetry; the proportion of the hexagon shaded in the bottom half is the same as that in the top, so I may as well just look at the top. (For a very similar reason, I’ve only labelled the left half.)
The semicircles have been replaced by their interesting diameters, the ones that are either vertical, or tangent to the slanted red edge.
Arbitrarily, I’ve chosen the side length of the hexagon to be 12 units, reasoning that that’s small enough to be manageable, but full of factors. I’ve called the horizontal edge of the parallelogram $2a$, and worked out that the blue-red overlap at the top is $12-2a$, making each half of it $6-a$. Similarly at the bottom, the overlap is $24-2a$, so each half is $12-a$.
A big shortcut
To find the shaded portion of the shape, I can divide the area of one shaded parallelogram by the area of the parallelogram formed by the marked edges (except for the slanted radii).
The area of the parallelogram is $2ah$, where $h$ is the height of the shape.
The area of the trapezium is $\frac{h}{2}((12+a) + (6+a))$, or $(9+a)h$.
So the fraction I want as my final answer is simply $\frac{2a}{9+a}$. Find $a$, and I have it! ((Knowing Cav’s answer, $a$ must be 4.))
Finding $a$
Finding $a$ comes down to three equations.
First, the height of the shape is $R+r$, but it’s also $6\sqrt{3}$ because the angle in the bottom left is $\frac{\pi}{3}$. That gives us $R + r = 6\sqrt{3}$ [1]
Secondly, the triangle formed by the edge marked $12-a$, the slanted $R$ and part of the red edge is half of an equilateral triangle; that tells us that $\frac{R}{12-a} = \frac{\sqrt{3}}{2}$ [2]
Lastly, using a circle theorem on equal tangents, the quadrilateral bounded by the two pink radii $r$, part of the red edge and part of the red-blue overlap, is a kite. Splitting it in half gives another half-equilateral triangle, and $\frac{r}{6-a}=\sqrt{3}$ [3]
Now for some clever rearrangement.
I can turn [1] into $\frac{r + R}{\sqrt{3}} = 6$.
I can turn [2] into $\frac{R}{\sqrt{3}} = 6 - \frac{a}{2}$.
And I can turn [3] into $\frac{r}{\sqrt{3}} = 6-a$.
That leads directly to $6 = 12 - \frac{3}{2}a$ and $a=4$.
Plugging back into the fraction, the shaded proportion is $\frac{8}{13}$, just as Cav got.
Oh hello, Sensei
“$0.\dot 61538\dot4$.”
“Playing the greatest hits, I see.”
Did you come up with a nicer way? I’d love to see it!