Centres of rotation
Ever since I’ve been teaching GCSE maths, I’ve struggled to explain one topic more than any other: how to find a centre of rotation.
There are several ways students approach this problem. There’s the “I dunno” way, sometimes disguised as “I dunno where to start.” This is the kind of comment that makes me wonder whether the student is making an effort at all.
It really doesn’t take that much effort to be in the second group, which says things like “Is it sort of twisted?” That’s not going to pick up many marks, but it shows a little bit of thought about the question.
The third group uses the right vocabulary, and says “It’s a rotation!”, confidently picking up one of the three marks. Some will even say “90º ((Degrees are rubbish, but they’re what the syllabus asks for)) clockwise” (or something similarly correct) for a second.
It’s the final mark that’s the problem: how do you find the centre of rotation? Obviously that’s straightforward if it’s a 180º rotation, but 90º presents a difficulty.
There’s a fourth group that calls for tracing paper and sets off on a dull process of stabby trial and improvement to find the centre. I have sympathy for this group; they generally pick up the marks, and that’s a Good Thing.
But it’s a bit unsatisfying for me, as a tutor, to recommend “tracing paper stabbity” as a method. Luckily, there’s a better way — and it involves one of the least-used tools in the geometry set: the 45º set square.
Here’s what you do
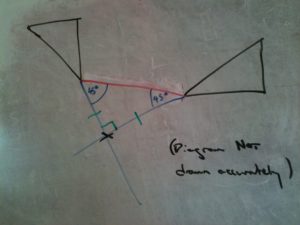
- Find two corresponding points on the original shape and the shape that’s been rotated — typically, the pointy end of the triangle, or a convenient right angle. Draw a line between them.
- At each of the points, draw a line at 45º towards where you thing the centre of rotation ought to be ((I’d use a set square, but constructing 45º lines would make examiners swoon.)) . Where these lines cross is the centre of rotation.
- Check you’ve gone the right way: measure the distance from your centre to two other corresponding points and check they’re the same. Otherwise, you need to draw your 45º lines on the other side of your line.
Why does it work?
The centre of rotation is a point that’s the same distance from any pair of corresponding points. If you draw a triangle using the two corresponding points and the centre, you get an isosceles triangle, with 90º at the centre of rotation. That means the other angles both have to be 45º.
Generalising to other angles
In likelihood, you’ll never need to find a centre of rotation outside of a GCSE exam, and by that standard 90º should be enough for anyone. But, just for the sake of argument, what if you had to find the centre of a 32º rotation? You can use the same principle: you need to build an isosceles triangle with 32º at the tip. You’ve got 148º left in your triangle, which need to be split equally between the other two angles: you’d draw lines at 74º to your original line.
In general, to find a centre of rotation with an $x$º angle, you’d need to draw angles of $\frac{180-x}{2}$ (or $90- \frac{x}{2}$) off of your original line.
* Edited 2017-07-21 to fix an unfinished sentence.