On Twitter, @RuedigerSimpson pointed me at an episode of My Favourite Theorem in which @FawnPNguyen mentioned a method for constructing $\sqrt{7}$:

  • draw a circle of radius 4
  • construct a perpendicular to the radius at a distance of 3 from the centre
  • the distance between the base of the perpendicular and where it meets the circle is $\sqrt{7}$, because $4^2 - 3^2 = 7$.

Very nice! The square root of any odd number can be constructed a similar way - $\sqrt{2n+1} = \sqrt{(n+1)^2 - n^2}$, by the difference of two squares.

Similarly, multiples of 4 are easy pickings: $\sqrt{4n} = (n+1)^2 - (n-1)^2$

Which leaves only numbers of the form $4n+2$ - which can’t be expressed immediately as the difference of two squares. But can such numbers be constructed similarly?

Bisection!

A simple way to construct, say $\sqrt{6}$ would be to construct $\sqrt{24}$ using the method above (a circle of radius 7 and a perpendicular 5 units away) and bisect the perpendicular. Since $\sqrt{6} = \frac{1}{2}\sqrt{24}$, we’ve got our distance!

But Simon didn’t like that. Can it be done without bisection?

No bisection!

I’m quite pleased with my alternative method, which I’m told is based on the Spiral of Theodorus, although it’s rather less involved.

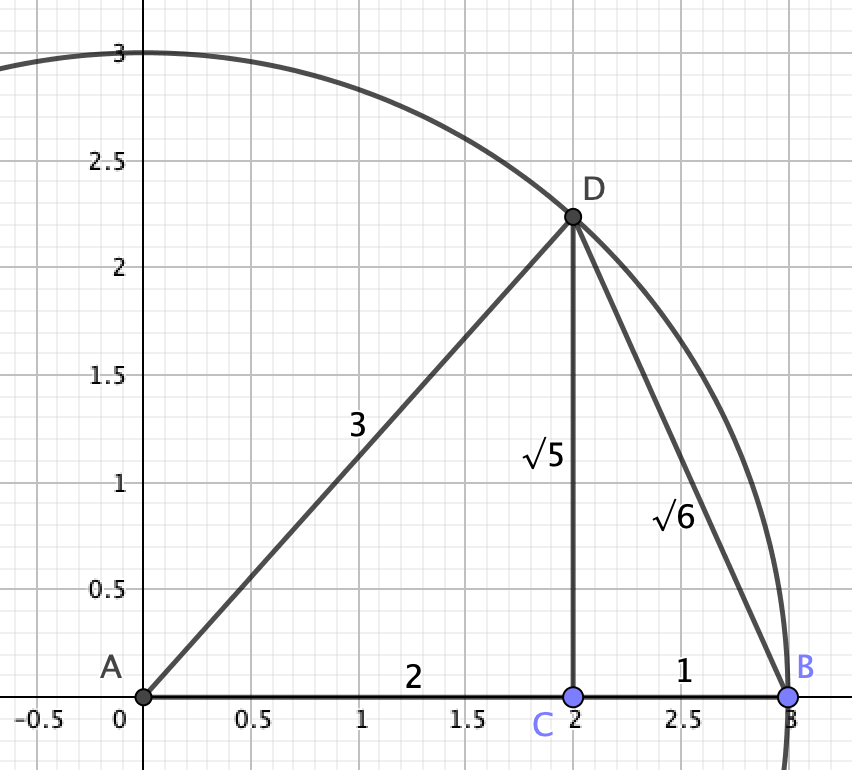
If you construct $\sqrt{5}$ using the method above, with a circle of 3 units and a perpendicular of 2, there’s a second right-angled triangle you can use: the one to the right of the perpendicular! The perpendicular has length $\sqrt{5}$, the base has length 1, so the hypotenuse has length $\sqrt{6}$!

I thought that was a neat bit of geometry. I don’t for a second imagine it’s new (it’s probably in Euclid if I could be bothered to look), but it was pretty enough a solution to make me grin.

Do you know of any other nice methods?