A curve-sketching challenge

Via @DrTrapezio, an interesting question:

Year 13 curve sketching challenge:

y = \| \| \| \|x\| - 1\| - 1\| - 1\|

— Luciano Rila (@DrTrapezio) July 14, 2016

Where do you even start with that mess? The answer to that, my friend, is you start in the middle and work your way out.

You can think of this thing as a series of transformations:

• Start with $y=|x|$
• Move it down one unit ¹ and take the modulus of the result
• Move it down one unit again and take the modulus of the result
• Move it down one unit one last time and take the modulus of the result

Put like that, it’s not so bad!

So, start with $y=|x|$: the classical V-shape with its vertex at $(0,0)$.

Move it down one unit, and it crosses the $x$-axis at $(\pm 1,0)$ and the $y$-axis at $(0,-1)$. The modulus of that would look like a W: it comes down from the top left, bounces at $(-1,0)$, bounces back down at $(0,1)$, and bounces back up at $(1,0)$ before heading up toward the top-right.

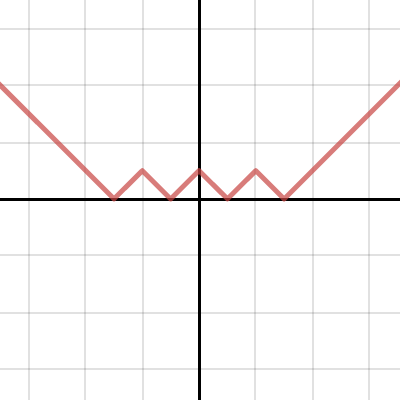
We could blindly repeat these steps a couple more times, but it’s worth having a little think here as we move the curve down a unit. All of the bottoms of the Vs now move to lie on the line $y=-1$, while all of the tops move to the $x$-axis. The curve crosses the axis at $(\pm 2,0)$. That all means that the curve zig-zags between $(-2,0)$, $(-1,1)$, $(0,0)$, $(1,1)$ and $(2,0)$, and heads upwards at either end.

By now the pattern should be fairly clear: the third shift-and-modulus will simply be a series of zig-zags starting at $(-3,0)$ and ending at $(3,0)$, with each peak on the line $y=1$ and each bottom on the $x$-axis.

And that’s exactly it:

Before you play with the sliders… what do you think they do?

* Edited 2016-10-03 to fix formatting

Footnotes:

1. translate it by one unit parallel to the negative $y$-axis