I… I… I…

*Looks up Ito’s Lemma*

*Reaches for bargepole, then doesn’t touch it.*

I… I… I…

Oh! It says here, there’s a thing called Ivory’s Theorem ((It’s also called Ivory’s Lemma.))!

What is Ivory’s Theorem?

Despite the main paper I could find about it calling it “the famous Ivory’s Theorem”, it was fairly tricky to pin down a definition for it; here is my understanding:

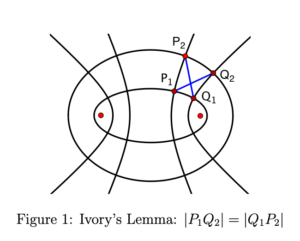
  • Let $F_1$ and $F_2$ be two points.
  • Let $E_1$ and $E_2$ be two ellipses, each with foci at $F_1$ and $F_2$
  • Let $H_1$ and $H_2$ be two hyperbolae, each with foci at $F_1$ and $F_2$
  • Let $Q$ be a ‘quadrilateral’ constructed from arcs of the four conics.
  • Then: the diagonals of $Q$ are of equal length.

For example:

Example of Ivory's Theorem

Why is it important?

Ivory’s Theorem was part of a larger calculation in which he calculated the gravitational potential due to a homeoidal shell – homeoidal (I just looked up) means “formed by two similar ellipsoids”. You could imagine the leather part of a rugby ball as homeoidal, and you wouldn’t be too far out.

It appears to be of use in determining the gravitational attraction between points, in general on two ellipsoids, but in particular on spheres. However, my tolerance for deciphering the 19th century prose of people like Kelvin and Pratt is fairly low just now. They seem enthused by it ((Feel free to explain it to me! The DOME is as much about ‘here’s an interesting thing, go and have a play with it!’ as it is about being a complete reference.))

Who was James Ivory?

Ivory (1765-1842) was the son, and namesake, of a Dundonian watchmaker, roughly contemporary with Gauss. He ran a mill in Forfarshire, although not very successfully; he spent his spare time studying the works of Lagrange and Laplace.

When the mill went into receivership in 1804, he became a professor at what was to become Sandhurst. He apparently suffered from depression throughout his later life, and believed his colleagues were conspiring against him. He died in 1842, in London.

* Updated 2019-09-01 to put in a missing image.