Heroic triangles

In a recent Maths Challenge, students were told the area of a triangle ($7$cm${}^2$) and the length of two of its sides ($6$cm and $8$cm), and asked how many possible lengths there were for the third side.

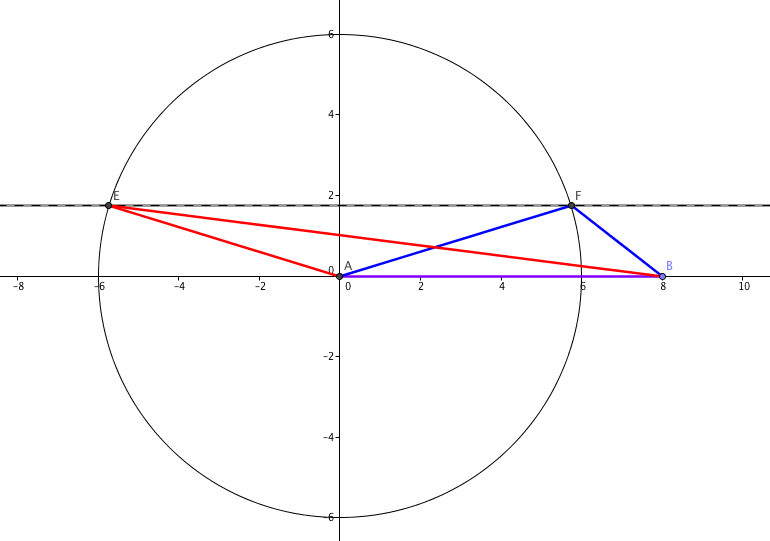
It’s easy enough to show there are two: let the base of the triangle $AB$ be the $8$cm side (purple). If the area of the triangle is $7c{m}^2$, the height of the triangle needs to be $\frac{7}{4}$cm (which is less than $6$cm); draw a line parallel to the base, $\frac{7}{4}$cm away from it (the dashed line) and draw a circle with radius $8$cm centred on one end of the base. Where the circle and line cross (at $E$ and $F$), you have a possible apex for your triangle.

However, my student misunderstood the question and thought she needed to find the possible lengths of the third side. That’s a substantially harder question - especially in a non-calculator exam! However, it is possible - and you can get an exact answer. It’s just tricky.

I need a Hero, holding out for a Hero ‘til the end of the night

You need to use a formula for the area of a triangle you may not have seen before, known as Hero’s formula. If the sides are $a$, $b$ and $c$:

$Area=\sqrt{S(S-a)(S-b)(S-c)}$, where the semiperimeter $S=\frac{a+b+c}{2}$

Let’s let $a=8$ and $b=6$. To make the sums a little easier, I’m going to call our missing side $2x$ - because that makes the semiperimeter a nice, manageable $S=7+x$.

The right hand side of Hero’s formula looks awful, but it simplifies quite nicely: $S-a$ works out to be $x-1$; $S-b=x+1$, and $S-c=7-x$.

So, squaring both sides and putting in 7 for the area: $49=(7+x)(x-1)(x+1)(7-x)$.

Do we have to multiply that out?!

Yup. Luckily, it’s easy if you spot you can use difference of two squares. $(7+x)(7-x)=49-x^2$, and $(x-1)(x+1)=x^2-1$.

That means we’ve got something a bit more manageable:

$49=(49-x^2)(x^2-1)$

That, we can multiply out:

$49=49x^2-49-x^4+x^2$, or (rearranging) $x^4-50x^2+98=0$

Oh no! It’s a quartic! These can be solved, in general, but we don’t need Cardano’s crazy formulas for this one, it’s a quadratic in disguise: we can just let $y=x^2$ to turn it into:

$y^2-50y+98=0$

Sadly, that doesn’t factorise, but you can complete the square and solve the traditional way:

$(y-25{)}^2-625+98=0$

$(y-25{)}^2=527$

$y-25=\pm \sqrt{527}$ ¹

$y=25\pm \sqrt{527}$

However, we made $y$ up - it’s really $x^2$:

$x=\sqrt{25\pm \sqrt{527}}$

And our side length is double that:

$x=2\sqrt{25\pm \sqrt{527}}$.

Obviously, you’d use a calculator if you had one - I certainly did - but the Mathematical Ninja probably wouldn’t. He’d say that $y$ was roughly $2.04$ or $47.96$, and take the square root to get something a bit more than $1.4$ and something a bit short of $7$ (it’s closer to $4\sqrt{3}$), making the side length a little more than $2.8$ or slightly short of $14$, both of which fit with our pictures! (The answers are 2.86 and 13.85, which isn’t too shabby for work in our heads).

Does it work for all triangles?

A natural question for a mathematician: can you use the same technique to answer all questions of this kind? The answer, surprisingly, is yes - as long as solutions exist! If you let $m$ be the mean of the sides you’re given ($m=\frac{a+b}{2}$)and $d$ be half the difference between them ($d=\frac{a-b}{2}$), the quartic ends up being $x^4-(m^2+d^2)x^2+(A+m^2{d}^2)=0$, where $A$ is the area.

If you were so inclined, you could work out a general formula for $x$- but I’ll leave that as an exercise!

Footnotes:

1. The square root of 527 is a smidge short of 23, of course. Off by about $\frac{1}{23}$, since you ask, so it’s $22.96$ or so.