An "Impossible" New Zealand exam: Part II
Last time, we looked at an ‘impossible’ question from a New Zealand exam, which was (of course) nothing of the sort.
The second question highlighted as a brute was this one:

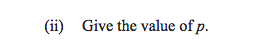

But, you see, I look at that and think… part (iv) isn’t straightforward on its own, but with the rest of the question - which doesn’t look too tricky - it ought to be ok. Shall we try?
Let’s.
So, part (i) asks us to find the height of point A - where $x=0$. We know that $y=\frac{x}{3}\br{x-p}+4$, and when $x=0$, $y=4$.
Part (ii) doesn’t present much more difficulty: we know point B has an $x$-value of 6 and a $y$-value of 4, so we can plug those in:
$4 = \frac{6}{3}\br{6-p}+4$, and $p$ has to be 6.
The full equation is $y=\frac{x}{3}\br{x-6} + 4$.
Sketching
Part (iii) asks us to sketch the graph, even though we’ve already got a decent picture of it. Let’s do as the people ask, shall we? We’ll plot the points we know at $(0,4)$ and $(6,4)$; the turning point is midway between and has a height of 1, so it’s at $(3,1)$.
We could, since we know the equation of the curve, find the $y$-values at $x=1$ and $x=2$ (which, by symmetry, are the values at $x=5$ and $x=4$, respectively).
When $x=1$, we get $y = \frac{1}{3}\times -5 + 4 = 2+\frac{1}{3}$.
When $x=2$, we get $y = \frac{2}{3}\times -4 + 4 = 1 + \frac{1}{3}$.
We can plot those in a nice smooth curve.
The comparatively tricky bit
Part (iv) asks us to find the width of the seat on a rope that miraculously doesn’t change the shape of the rope, which is itself miraculously not following the catenary shape that dangling ropes generally follow. As Mark Twain almost said, when a rope behaves like that, it should be made to explain itself.
But OK, let’s assume that there’s some bizarre feat of engineering that makes this possible and we need to solve this at the resulting exhibit in the New Zealand Museum Of Improbable Science.
We have $1.2 = \frac{x}{3}\br{x-6} + 4$, which I would begin by rearranging. I don’t fancy the 3, so I’ll multiply through by it:
$3.6 = x(x-6)+12$
Let’s expand the brackets and subtract 3.6 from each side:
$0 = x^2 - 6x + 8.4$
Now, I presume, since it asks for answers to two decimal places, that this exam permits calculator use, in which case I would recommend using the quadratic formula to find $x = \frac{6 \pm \sqrt{36 - 33.6}}{2} = 3 \pm \sqrt{\frac{3}{5}}$. Those are 3.7745… and 2.2254…, which are 1.55m apart, to two decimal places.
(Personally, I’d prefer to spot that the solutions were $2\sqrt{\frac{3}{5}}$ apart, turn it into $\frac{1}{5}\sqrt{60} = \frac{1}{10}\sqrt{240}$, and use the fact that $\sqrt{240.25}=15.5$ to get the right answer without reaching for a calculator. But I appreciate, I’m not a Year 11 student.)
Complaining that an exam is impossible when it’s just hard means you will be taken less seriously in the rare cases when boards do, inadvertently, set impossible questions. Don’t do it.