The Mathematical Ninja finds the value of $\pi$
This article has also been published as part of the Relatively Prime zine.
The student yelped, and found his wrists and ankles strapped to the wheel before the lesson had even started.
“Good morning,” said the Mathematical Ninja. “I think you and I need to have a little… talk.”
The first knife landed between the student’s fingers. “Bu-bu-bu…”
“Do keep still, won’t you? I’d hate for anything to go wrong with this demonstration, which I will undertake while blindfolded.”
A whimper of understanding.
“Now, I gather you have been writing to anyone whose address you can get hold of ((See http://www.acmescience.com/2012/07/spot-the-error/)) to claim that $\pi = \frac{14 - \sqrt{2}}{4} \approx 3.146446$.”
“But it mfff.”
“Lucky that was a custard pie rather than a knife, eh? You see, there are very many problems with your method, any one of which I could pick apart. However, I’m going to cut… (I heard you flinch there. Very bad idea.) I’m going to cut straight to the chase and show you how to use pretty basic maths to work out the value of π.”
“Mf.”
“No, you’re wrong by about 0.005, and I’ll show you why your value can’t be π. Let’s start with a very rough example to get the idea straight: consider a 3-4-5 triangle. You’re familiar with it? Excellent. Can you see this picture? Of course not, your face is covered in custard pie. Let me get the hose. Better?”
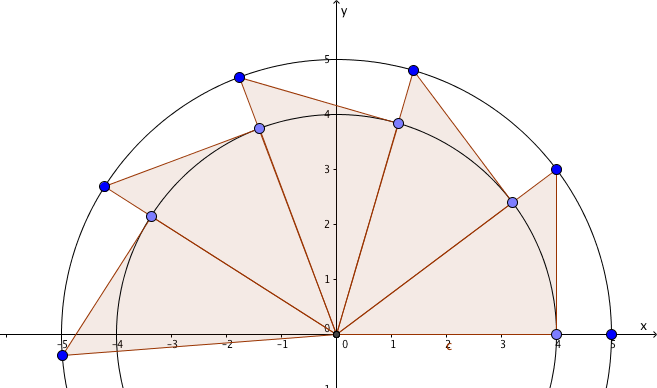
“Cold? It can’t be that cold, it’s liquid. I can warm you up if you like, I have a flame-thrower? No? OK. Where were we? Ah, yes. So, you can see that when I place copies of this triangle point to point, it takes five of them to reach the negative x-axis, agreed? That’s easy enough to prove with the compound angle formula for tangent.”
“I’m not a mathmf.”
“That sounded like an apple pie. You really are a lucky man. I’ll make a proof of that elsewhere. In any case, four of these triangles lie wholly within a semicircle of radius 5, which has an area of $\frac{25}{2}\pi$. The triangles each have an area of six, so $24 \lt \frac{25}{2}\pi$, and $\pi \gt \frac{48}{25} = 1.92$. Similarly, five of them lie outside the circle with radius 4, which has area 8π, so $30 \gt 8\pi$ and $\pi \lt \frac{30}{8} = 3.75$.”
“I don’t see how that invalidates my’ll shut up now.”
“You’re right, to an extent: your value of π does lie within these less-than-impressive limits. However, there’s nothing particularly special about a 3-4-5 triangle, any right-angled triangle would work just as well.”
“You’re going to do it with smaller triangles?” whimpered the student.
The Mathematical Ninja idly threw three darts into the gap between the student’s arm and ear, muttering “one hundred and EIGHty, pretty much the only time you should say that when looking at a circle” under his breath.
He continued, sharpening an axe. “So, let’s try a triangle with a base of 1,000,000 units and a height of 1.”
“And an area of 500,000 square units!” offered the student.
The Mathematical Ninja glared. “It turns out, if you do the sums, you need between 3,141,592 and 3,141,593 of these triangles. Those numbers look familiar? Now, the outer semi-circle has an area of $\left(\frac{1}{2}+5 \times 10^{11}\right)\pi$, and completely contains 3,141,592 triangles, each with area $5 \times 10^{5}$, which means $\left(\frac{1}{2}+ 5 \times 10^{11}\right)\pi \gt \left(3,141,592\right)\left(5 \times 10^{5}\right)$, so $\pi \gt 3.141592$ – minus a tiny fraction I’ll ignore .”
He paused, and the student said nothing. This didn’t invalidate his number, but he could see where it was going.
“Similarly, the inner semi-circle has an area of $5 \times 10^{11} \pi$ and is completely contained by 3,141,593 triangles. That means $5 \times 10^{11} \pi \lt \left(3,141,593\right)\left(5 \times 10^{5}\right)$, and $\pi \lt 3.141593$. I’m afraid that rather does exclude your value of π as the ratio of the radius of a unit circle to its area, doesn’t it?”
“Surely,” said the student, finding his tongue at last, “you don’t expect me to take those numbers on trust?”
“No, Mr Reddy,” said the Mathematical Ninja, “I expect you to pie.” Splat. “And don’t call me Shirley.”