The Mathematical Pirate and the Formula Triangle
The Mathematical Pirate took one look at the piece of paper attached to the dock.
“They’re BANNING formula triangles?! By order of @srcav?!” He swished his sword around. “Let me figure out where he lives, I’ll show him.”
“He lives… inshore, cap’n” said the $n$th mate. “It’s too dangerous.”
“Can we send Ninja-chops?” He was pretty sure the Mathematical Ninja wasn’t within earshot, but lowered his voice all the same.
“I’ll see what we can do,” said the $n$th mate.
The scene went wibble-wibble-wibble as the Mathematical Pirate thought back to his time at Pirate Maths school. The Pirate Teacher was sneakily asking physics questions: “What’s the potential difference? You, yes, you?”
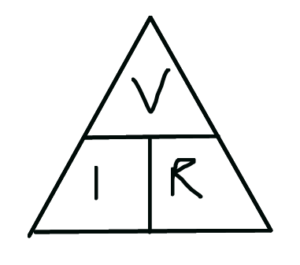
“$V$?” said the young Mathematical Pirate. “… Aye! Arrr!”
“Well done,” said the Pirate Teacher. “$V = IR$. So what’s $I$? You, there!” He pointed at the $n$th mate.
“$\frac{V}{R}$,” he said without even a beat.
“Blistering barnacles!” said the Mathematical Pirate. “How did you rearrange that so quickly?”
The $n$th mate drew out a formula triangle, like this:
“How does that help?”
“If two things are on the same line, you can multiply them together to get the other.”
“So, $V=IR$. I knew that.”
“But if they’re on different lines, you can divide the top one by a lower one to get the third.”
“So $I = \frac{V}{R}$, like you said.”
“Exactly. And it works any time you have $a = bc$ (whatever is alone goes on top) or $d = \frac{e}{f}$ (whatever’s on top stays on top) - so you can use it for SOH CAH TOA, density, speed, constant acceleration… all of the things you need in your day-to-day pirating adventures.”
“Arr,” said the Mathematical Pirate. “I think I’ll steal that.”
The Mathematical Pirate is a passionate - you might say violent - advocate of the formula triangle, but it’s not as well-received - generally - among teachers, several of whom would ban them given the chance. There are reasons for this antipathy, some better than others - which I thought I’d put to the Mathematical Pirate.
I don’t like them
“Arr. That’s just stupid,” said the Mathematical Pirate. “I don’t like the difference of two squares (just learn to factorise properly!) but I realise it works for some people. They’re welcome to use it. Doesn’t bother me. I’m a pirate, not a fascist.”
“Right”, I said, “you could make the same argument about learning $7 \times 8 = 56$ when you ‘should’ be working it out as $(10-2) (10-3)$ every time.”
They can go wrong
The Mathematical Pirate tapped his cutlass, absent-mindedly, on the table. “And algebra never does, I suppose?”
“They say algebra, done properly, is infallible.”
A derisive snort. “A formula triangle, used appropriately, works just fine. It’s based on algebra.”
They’re gimmicky
“@shahlock says he doesn’t teach them because they’re gimmicky, like singing the quadratic equation.”
The Mathematical Pirate looked slightly hurt. “That’s my favourite shanty! Hoist up the minus b’s sails! See how the square root’s set!”
“Ahem.”
“Erm… yeah, sorry. Is that one of those Nix the Tricks arguments? That gimmicks are harmful and we should only work from a spirit of true understanding? Because that’s bollocks in the real world.”
“Language!”
“Oh!” said the Mathematical Pirate. “C’est débile en réalite.”
“That’s better. I agree, in an ideal world, every student would generate the rules of algebra starting from a few self-evident axioms and apply them rigorously to appropriate problems, but that’s not how it works, however much we’d like it to. ‘Gimmicks’ like the triangle, the Table of Joy ((See Basic Maths For Dummies, available at all good bookstores and some rotten ones)) , subtracting simultaneous equations, difference of two squares, and dozens of others, make some problems accessible to students who’ll otherwise get discouraged and think “I’ve no idea what’s going on here, I must be stupid and rubbish at maths.”
“Arr.”
They avoid understanding and cementing algebraic skills
“Wait, what?” said the Mathematical Pirate. “The mechanical shuffling of abstract symbols around an equals sign somehow shows more ‘understanding’ than setting up a triangle? Give me a break.”
“Well, I’m sure some teachers would argue that students ought to know what the equals sign means, and that whatever you do to one side you need to do to the other.”
“They ought to, aye,” said the Mathematical Pirate. “And I can see that it’s just for a special case - but it’s a special case that crops up ALL THE SODDING TIME.”
“Thinking about it, there’s one big distinction that got missed in the whole twitter spat the other day: the difference between numeracy and maths. The triangle is a great tool for numeracy: it gives you the right answer quickly. It’s not quite so great if you’re trying to train a mathematician (or someone who’ll use mathematical skills for science or whatever) as they really ought to be able to rearrange.”
“But does that mean they avoid understanding?”
“I use formula triangles to rearrange things all the time, especially something like $a = \frac bc$ - if I want $c$, I can visualise the triangle much more quickly than multiplying by $c$ and dividing by $a$. And I like to think that I understand algebra pretty well, thank you very much.”
They avoid interconnectivity
“So, one method that works for problems across maths, physics, chemistry, biology, economics, navigation and 3,000 other things is somehow anti-connectivity? I don’t get it.”
“I think the argument is that using a triangle isn’t connected to the rest of algebra.”
“Except that it’s based on algebra and a nifty way of dealing with a special case, like all the ones we outlined earlier? Except that it gives a second check on an algebraic method? Except that it gives students a hook to see that algebra works the same way as another method they’re comfortable with?”
“I know. The whole thing smacks of people wanting to teach the One True Path To Mathematics - but there’s no such thing. By necessity, maths teaching involves a hodge-podge of methods that start out as mystical recipes before eventually, with any luck, taking part of a strong mathematical structure.”
They eliminate the need for thinking
“Arrr!” said the Mathematical Pirate. “That they do. I’ve got better things to do with my brain than think about the mechanics of simple algebraic equations. Like give sanity checks to my answers. The first thing I learned in my navigation PhD was that the correct order of thinking is a: dredge it up from memory, b: look it up; c: work it out. That frees your brain up to do important things like interpret the question, interpret the answer, swash buckles, and so on.”
“Isn’t the whole point of maths to make things simpler? Saying ‘thou shalt rearrange’ feels like one of those arbitrary school rules that, even though there might have been good reasons for putting them in place, just serve to annoy people and end up being ignored.”
“Rules?” said the Mathematical Pirate, with a quizzical look on his face.
“In any event, taking a perfectly valid method a student knows how to use and labelling it ‘wrong’ is a sure-fire way to kill their confidence and mathematical creativity.”
They’re not proper maths
The cutlass handle wobbled, as its blade was several centimetres deep in the fo’c’s’le. “Arr,” said the Mathematical Pirate, “I’ll never get that out now. Proper maths? PROPER MATHS? Exploiting a recurring pattern isn’t proper maths?” He breathed out.
“I know, I know. It’s a bizarre argument: one of the main ideas of ‘proper’ maths is to take something tricky, spot a pattern you know how to deal with, and use it to make the tricky thing simpler.”
“Hello, the @srcav residence?” said the voice on the phone.
“The Mathematical Pirate tells me you want to ban formula triangles.”
“… well, not nece…”
“SHUT IT! They’re not my preferred way of doing things, either. But they’re really useful to some students.”
“I didn’t me…”
“THE MATHEMATICAL NINJA HAS SPOKEN.”
Click.
* Edited 2014-10-15 to put in missing image, and again to stop the author confusing Ninjas with Pirates.