A MathsJam Masterclass

At the East Dorset MathsJam Christmas party, @jussumchick (Jo Sibley in real life) posed the following question:

There are two ways to draw a 16-gon with rotational symmetry of order 8 inside a unit circle, as shown. What’s the ratio of their areas?

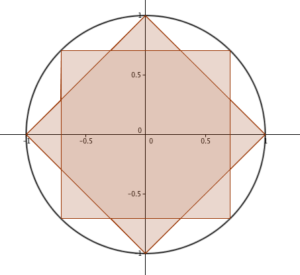
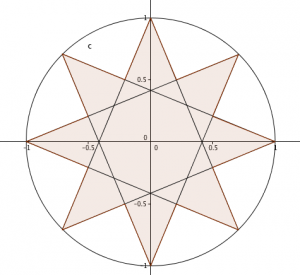Typically, I look at this sort of question and sigh: it’s going to need a (shudder) calculator to work out the lengths of the various sides, and the areas will be really ugly numbers… but I was assured the answer was ‘something nice’. So, I put down my mince pie and picked up a pen. (For the sake of narrative, I’ve covered up some of my mistakes.)

The splitting up of the shape

My first step was to notice that I could split each of the shapes into 16 congruent triangles – from the centre of the circle (O) to a point on the circle (A), to one of the ‘elbows’ (B) between the circle points. In the 16-gon made of two squares, the angle OAB is $\frac{1}{4}\pi$, as it’s half of a right-angle. The angle BOA is $\frac{1}{8}\pi$, because it’s a sixteenth of a circle, and the final angle ABO is $\frac{5}{8}\pi$. In the other 16-gon, angle BOA is $\frac{1}{8}\pi$, like before; ABO is easy to find, too – if you continue OB through B, the other side of the angle is $\frac{1}{4}\pi$ – so ABO has to be $\frac{3}{4}\pi$. OAB turns out to be $\frac{1}{8}\pi$ as well. In each case, the side opposite the largest angle is 1 – the radius of the circle.

An alternative area formula

Every Core 2 student knows what to do from here: work out another side using the sine rule, then use $Area=\frac{1}{2}ab\sin (C)$ to find the areas, multiply them by 16 and get the ratio. Full marks, next question. And a gaping void in your soul, of course, but you don’t lose marks for that. What a mathematician does is, find a formula for the area of the triangle that works directly from the information we have: a side and three angles. It’s not too tricky: the sine rule says $b=\frac{\sin (B)}{\sin (A)}a$, so $\frac{1}{2}ab\sin (C)=\frac{1}{2}{a}^2\frac{\sin (B)}{\sin (A)}\sin (C)$ or, if we’re tidy-minded, $\frac{a^2\sin (B)\sin (C)}{2\sin (A)}$, which has a nice symmetry to it. (Incidentally: I had this formula wrong to begin with; my $\sin (A)$ and $\sin (C)$ were transposed. It smelt funny: there’s no real difference between angles B and C, so it didn’t make sense for them to be divided rather than multiplied).

Now you work out the areas, right?

Nope. Don’t care about the areas. I care about their ratios. If I set up the triangles so that my $a$ is 1 in both cases, I want the ratio: $\frac{\sin \left(\frac{1}{8}\pi \right)\sin \left(\frac{1}{4}\pi \right)}{2\sin \left(\frac{5}{8}\pi \right)}:\frac{\sin \left(\frac{1}{8}\pi \right)\sin \left(\frac{1}{8}\pi \right)}{2\sin \left(\frac{3}{4}\pi \right)}$ How lovely! We can simplify it immediately by dividing both sides by $\frac{1}{2}\sin \left(\frac{1}{8}\pi \right)$ to get: $\frac{\sin \left(\frac{1}{4}\pi \right)}{\sin \left(\frac{5}{8}\pi \right)}:\frac{\sin \left(\frac{1}{8}\pi \right)}{\sin \left(\frac{3}{4}\pi \right)}$ Multiply everything through by $\sin \left(\frac{5}{8}\pi \right)$ and $\sin \left(\frac{3}{4}\pi \right)$ to get: $\sin \left(\frac{1}{4}\pi \right)\sin \left(\frac{3}{4}\pi \right):\sin \left(\frac{1}{8}\pi \right)\sin \left(\frac{5}{8}\pi \right)$ – and the left-hand-side works out to be $\frac{1}{2}$. The right-hand-side… well, I’d understand reaching for a calculator… but you really don’t need to! It turns out that $\cos (A-B)-\cos (A+B)\equiv 2\sin (A)\sin (B)$, which means you can rewrite the right hand side as $\frac{1}{2}(\cos \left(\frac{1}{4}\pi \right)-\cos \left(\frac{1}{2}\pi \right))=\frac{1}{2}(\frac{1}{\sqrt{2}}-0)$, so our ration is: $\frac{1}{2}:\frac{1}{2\sqrt{2}}$, or, more neatly, $\sqrt{2}:1$. What do you know? It was a nice number after all!