The marvellous @solvemymaths tweeted some time ago about finding least common multiples and highest common factors:

I broadly agree with Ed - I have an antipathy towards Venn diagrams that’s probably more fierce than they deserve. The tweet got me thinking about how I think about LCM and HCF calculations. I’m going to pick two sizeable numbers, 768 and 480, for my example.

Generate the factors

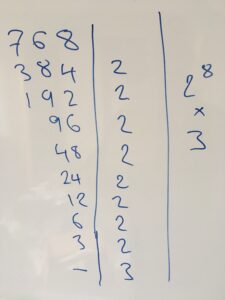
There are all sorts of methods for doing this, and I don’t really care about the details. Here’s the way I instinctively did it on the whiteboard - you might prefer a tree, or more working. Doesn’t matter. Give me a correct prime factorisation and I don’t care if it was whispered into your ear by the ghost of Fermat.

Factors of 768Factors of 480

So I’ve worked out that $768 = 2^8 \times 3$ and that $480 = 2^5 \times 3 \times 5$

A note on language

The language of ‘least common multiple’ and ‘highest common factor’ is counterintuitive, but correct: the one with ‘highest’ in is less than the one with ‘least’ in. That’s because factors are never bigger than the number you’re working with, and multiples are never smaller. So: it’s worth focussing on the kind of number you want rather than the words highest and least. It will trip people up.

LCM

LCM calculation

The least common multiple is the smallest number that you can divide by both of your examples. Its prime factorisation must include all of the factors of both numbers. So, we look at all of the powers-of-a-prime factors of each number in turn, and pick whichever one has the bigger power (or, if it’s a tie, the number in question).

Here, that’s $2^8$, $3^1$ and $5^1$, so the LCM is $2^8 \times 3^1 \times 5^1$, which is $128 \times 3 \times 5 = 3,840$.

HCF

HCF calculation

The highest common factor is the biggest number that divides into both of your example; in this case, we look at each power-of-a-prime factor and pick the smaller power. Again, if it’s a tie, we just take the common number; if a factor appears in one number but not the other, we ignore it. For this one, it’s $2^5$ and $3^1$. (If you’re uncomfortable with ditching the 5, you can consider 768 as having a factor of $5^0$.)

Working it out, that gives $32 \times 3 = 96$ as the highest common factor of both.