It’s encouraging to see a few less-predictable questions coming up in the new GCSE and A-level specifications. @mathsjem highlighted an especially nice GCSE one:

This is unusual more than it is tricky: $x = 1.0\dot2 = \frac{92}{90}$ and $y = 0.\dot 4 = \frac 49$, so $x-y = \frac{92-40}{90} = \frac{52}{90} = \frac{26}{45}$.

However, it spawned an interesting offshoot discussion with @richstakes, who asked “Can you subtract $0.\dot4$ from $1.0\dot2$ to get $0.5\dot7$? Where do you start?”

It’s a good question. Laid out traditionally, you have

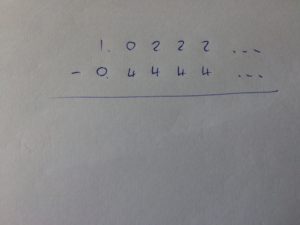IMG_1655 and there’s no right-hand end to borrow from.

Obviously, ‘doing it with fractions’ is the way I’d like to see it done. But can it be done arithmetically? You bet.

One possibility is the ‘look ahead’ method, which starts from the left and says:

1-0 would normally be fine, but we’ll need to lend one to the right, giving us: 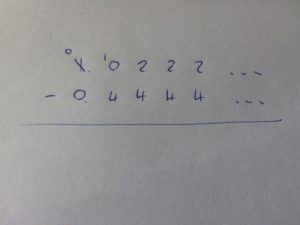IMG_1656

10-4 would be fine, but we’ll need to lend one to the right:

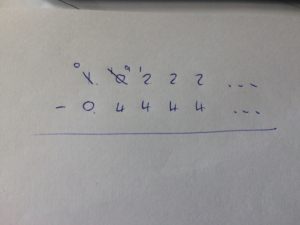
IMG_1657

Similarly, 12-4 would be fine, but we’ll need to lend one to the right:

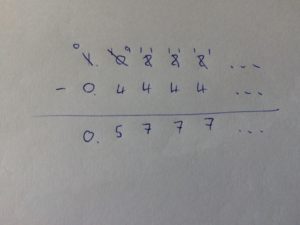
IMG_1660

And the pattern continues from here – each 2 is replaced with an 11, leaving us $0.5\dot7$. Phew.

I’m not a fan of this method, not just because it’s a pain in the decimal point to typeset. If you’re happy to accept that $0.\dot9 = 1$ (because it does, dagnabbit), there are a couple of alternatives.

The first is to make the $0.\dot4$ up to 1 by adding $0.\dot5$ to both numbers. Then we have $1.5\dot 7 - 0.\dot9$, which (because dagnabbit) is $0.5\dot7$.

The second, very similarly, is to bring the $1.0\dot2$ down to 1 by subtracting $0.0\dot2$ from each. This gives $1 - 0.4\dot2$ and – because dagnabbit – you can write that as $0.\dot 9 - 0.4\dot 2 = 0.5\dot7$ again.

This is, of course, all a bit handwavy; however, it can be formalised using geometric series if you’re so inclined. That said, it’s an awful lot easier to do it with fractions and avoid all of this recurring decimal nonsense.