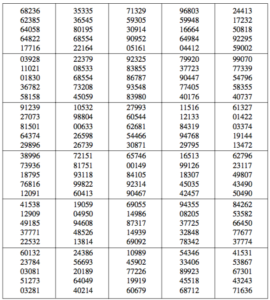
If you flick to the back of an old A-level formula sheets, you might spot a list of random digits like this one from an MEI book:

random number table

Why on earth would you want random numbers?

There are all sorts of reasons one might want a set of random numbers: perhaps you have a large set of data and want to pick out a random subsample of it - you need a source of random numbers. Perhaps you have a simulation you want to run, with random parameters - you need a source of random numbers. Perhaps you want to play a game of Snakes and Ladders but your three-year-old has eaten the dice…

Hang on a second. Be right back.

Nowadays, of course, you could just go to random.org and ask for a bespoke selection of artisanal random numbers, such as a selection of $n$ from a list with or without replacement, lottery numbers, and so on. Generated by fluctuations in the atmosphere, I’m told. Haughty sniff. Fine, if you want to get random number from… physics, go ahead, be my guest.

A battery of tests

I don’t know how MEI (or anyone else) generated their random digits - but I do know that they are submitted to a rigorous series of tests to make sure they’re properly random.

Which is a bit of a head-scratcher: after all, the set of digits 1111…. is just as likely as any other set of the same length. However, there are tests for what one would expect a large number of random digits to look like. For example:

  • Frequency: Every digit would appear roughly the same number of times.
  • Serial: Every pair of digits appears roughly the same number of times.
  • Poker: The patterns in sets of five digits appear in roughly the right frequency.
  • Gap: The gaps between zeros (or any other digit) are distributed correctly.

There are many others, of increasing sophistication, with names like Kolmogorov-Smirnov, Wald-Wolfowitz, and The Diehard Tests - but at a minimum, a useful set of random numbers will pass the four tests above.

Selecting a sample

Suppose we want a sample of ten people from a population of 450 conveniently-labelled individuals (from 0 to 449). Doing it the old-fashioned way, we could use the random number table to generate the appropriate labels.

Given a big table of random numbers, you should pick your starting position at random. Because it is currently 4:04, I shall pick the fourth box in the fourth column as my starting point.

I then go down, row by row, taking the first three digits of each row, rejecting any that are at least 450, until I have ten:

165 991 (reject) 183 450 (reject) 424 943 (reject) 082 377 328 783 (reject) 543 (reject) 334 899 (reject) 455 (reject) 687 (reject and start the next colum) 244 172 (… the next eight require rejecting …) 407

So, the selection for our sample is 165, 183, 424, 082, 377, 328, 334, 244, 172 and 407. Don’t try to tell me you’d rather have a website do that for you!

Kish grids

An interesting problem comes up in telephone surveys: if you always interview the person who answers the phone, you incur a bias towards phone-answerers.

A method developed to avoid this is the Kish grid, which works as follows.

  • For your $k$th call in the survey:
  • Ask how many eligible people live in the household (call it $n$).
  • Assign each person a number in order of age, starting with one.
  • For each house, calculate $k \pmod{n}$. (For the purposes of the survey, a remainder of 0 counts as $n$).
  • Interview that numbered person in the list.

(Telephone surveyors, however, tended to have a grid available that would tell them which person to ask for - apparently not everyone likes doing division on the fly mid-call ((Am I unusual? I would be more freaked out by the phone call than the division.)) !)

This is quite neat - in the long term, every member of an $n$-person household is equally likely to be picked, although there is a slight bias in favour of young people.

So there you go. Hopefully that counts as an interesting post about random numbers tables!