A couple of puzzles that came my way via @srcav today:

Cav’s solutions to this one are here; mine are below the line further down.

And to this one, here

Have a go yourself before you read on!

I’ve mentioned before about @solvemymaths and @cshearer41 puzzles: they usually consist of two puzzles. First, finding an answer; secondly, finding a method that makes you go ‘oo!’.

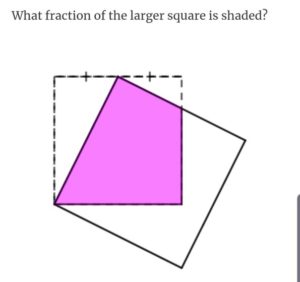
Area 48

  • The white triangle at top-left is $\frac{1}{4}$ of the smaller square.
  • The white triangle at top-right is $\frac{1}{16}$ of the smaller square (similar triangles)
  • So the pink shape is $\frac{11}{16}$ of the smaller square.
  • The larger square has side length $\frac{\sqrt{5}}{2}$ as long as the smaller square (via Pythagoras)
  • So its area is $\frac{5}{4}$ as large.
  • Therefore, the pink shape is $\frac{11}{16} \div \frac{5}{4} = \frac{11}{20}$ of the larger square.

Angle puzzle

My first thought, faced with this, was “I really can’t be bothered chasing all those angles. Surely there’s some symmetry to exploit?”

Surely there is.

angles setup angles solution

  • All of the points on the outside of the squares lie on a circle (by symmetry). This circle has the same centre as the one going through the points of the pentagon.
  • The red lines divide the angle at the centre of the circles into fifths - so the angle between the two outer red lines is thus $\frac{4}{5}\pi$.
  • The angle subtended at the circumference yadda yadda - the angle between the two black lines is $\frac{2}{5}\pi$.
  • So the original shaded angle is $\frac{8}{5}\pi$ (or 144 degrees, if the Ninja isn’t looking).

Nice puzzles!